
【題目】已知一個零刻度落在點A的量角器(半圓O)的直徑為AB,等腰直角△BCD繞點B旋轉.
(1)如圖1,當等腰直角△BCD運動至斜邊BD交量角器邊緣于點G,直角邊CD交量角器邊緣于點E,F,第三邊交量角器邊緣于點H時,點G在量角器上的讀數為20°,求此時點H在量角器上的讀數.
(2)如圖2,當點G,E在量角器上的讀數α,β滿足什么關系時,等腰直角△BCD的直角邊CD會與半圓O相切于點E?請說明理由.

【答案】(1)、110°;(2)、β=![]() α+45°
α+45°
【解析】
試題分析:(1)、連接OG、OH.由題意可知:∠AOG=20°,由等腰直角三角形的性質可求得∠CBD=45°,接下來,依據圓周角定理可求得∠HOG=90°,最后依據∠AOH=∠AOG+∠GOH求解即可;(2)、連接OG、OE.先由切線的性質證明OE⊥DC,然后依據平行線的判定定理可證明EO∥CB,接下來依據平行線的性質和可得到∠EOA=∠CBA,最后結合圓周角定理以及∠ABC、∠ABG、∠DBC的關系可得到α、β的關系.
試題解析:(1)、如圖1所示:連接OG、OH.
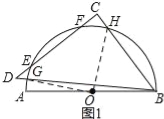
∵點G在量角器上的讀數為20°, ∴∠AOG=20°. ∵△BCD為等腰直角三角形,
∴∠CBD=45°. ∴∠HOG=90°. ∴∠AOH=∠AOG+∠GOH=20°+90°=110°.
(2)、如圖2所示:連接OG、OE.
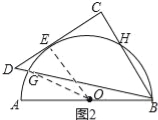
∵DC為圓O的切線,E為切點, ∴∠OED=90°. ∴∠OED=∠C. ∴EO∥CB.
∴∠EOA=∠CBA=β. 又∵∠GBA=![]() ∠GOA=
∠GOA=![]() α,∠ABC=∠ABG+∠DBC, ∴β=
α,∠ABC=∠ABG+∠DBC, ∴β=![]() α+45°.
α+45°.


科目:初中數學 來源: 題型:
【題目】近年來,某市旅游事業蓬勃發展,吸引大批海內外游客前來觀光旅游.下面的兩副圖分別反映了該市從2003年到2006年游客總人數和旅游業總收入的情況:

根據統計圖提供的信息,解答下列的問題:
(1)2006年游客總人數為__________萬人次,旅游業總收入為_________萬元;
(2)在2004、2005、2006年這三年中,旅游業總收入增長幅度最大的是________年,這一年的旅游業總收入比上一年增長的百分率為________(精確到0.1%);
(3)在2006年的游客中,國內游客為1200萬人,其余為海外游客.據統計,國內游客的人均消費約為700元,海外游客的人均消費約為多少元?(注:旅游收入=游客人數×游客的人均消費)
查看答案和解析>>
科目:初中數學 來源: 題型:
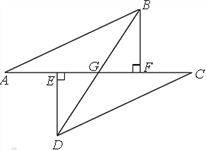
【題目】如圖所示,點A、E、F、C在同一直線上,AE=CF,過E、F分別作DE⊥AC,BF⊥AC,且AB=CD,
(1)AB與CD平行嗎?若平行請說明理由;
(2)證明BD平分EF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】手機微信推出了搶紅包游戲,它有多種玩法,其中一種為“拼手氣紅包”:用戶設定好總金額以及紅包個數后,可以生成不等金額的紅包.現有一用戶發了三個“拼手氣紅包”,隨機被甲、乙、丙三人搶到.
(1)以下說法中正確的是
A.甲、乙兩人搶到的紅包金額之和一定比丙搶到的紅包金額多
B.甲一定搶到金額最多的紅包
C.乙一定搶到金額居中的紅包
D.丙不一定搶到金額最少的紅包
(2)記金額最多、居中、最少的紅包分別為A,B,C,試求出甲搶到紅包A的概率P(A).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是△ABC的BC邊上的一點,∠B =40°,∠ADC=80°.
(1)求證:AD=BD;
(2)若∠BAC=70°,判斷△ABC的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖①,OP是∠MON的平分線,點A為OM上一點,點B為OP上一點.請你利用該圖形在ON上找一點C,使△COB≌△AOB,請在圖①畫出圖形.參考這個作全等三角形的方法,解答下列問題:
(2)如圖②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分別是∠BAC、∠BCA的平分線,AD、CE相交于點F.請你寫出FE與FD之間的數量關系,并說明理由;
(3)如圖③,在△ABC中,如果∠ACB不是直角,而(1)中的其他條件不變,在(2)中所得結論是否仍然成立?請你直接作出判斷,不必說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區在一次九年級數學做了檢測中,有一道滿分8分的解答題,按評分標準,所有考生的得分只有四種:0分,3分,5分,8分.老師為了了解學生的得分情況與題目的難易情況,從全區4500名考生的試卷中隨機抽取一部分,通過分析與整理,繪制了如下兩幅圖不完整的統計圖.
請根據以上信息解答下列問題:
(1)填空:a= ,b= ,并把條形統計圖補全;
(2)請估計該地區此題得滿分(即8分)的學生人數;
(3)已知難度系數的計算公式為L=![]() ,其中L為難度系數,X為樣本平均得分,W為試題滿分值.一般來說,根據試題的難度系數可將試題分為以下三類:當0<L≤0.4時,此題為難題;當0.4<L≤0.7時,此題為中等難度試題;當0.7<L<1時,此題為容易題.試問此題對于該地區的九年級學生來說屬于哪一類?
,其中L為難度系數,X為樣本平均得分,W為試題滿分值.一般來說,根據試題的難度系數可將試題分為以下三類:當0<L≤0.4時,此題為難題;當0.4<L≤0.7時,此題為中等難度試題;當0.7<L<1時,此題為容易題.試問此題對于該地區的九年級學生來說屬于哪一類?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深圳沙井某服裝廠2017年銷售額為8億元,受中美貿易戰影響,估計2019年銷售額降為5.12億元,設平均每年下降的百分比為x,可列方程為( )
A.8(1﹣x)=5.12B.8(1+x)2=5.12
C.8(1﹣x)2=5.12D.5.12(1+x)2=8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com