
【題目】如圖,矩形OABC的頂點A、C分別在![]() 的正半軸上,點B的坐標為(3,4)一次函數
的正半軸上,點B的坐標為(3,4)一次函數![]() 的圖象與邊OC、AB分別交于點D、E,并且滿足OD= BE.點M是線段DE上的一個動點.
的圖象與邊OC、AB分別交于點D、E,并且滿足OD= BE.點M是線段DE上的一個動點.
(1)求b的值;
(2)連結OM,若三角形ODM的面積與四邊形OAEM的面積之比為1:3,求點M的坐標;
(3)設點N是![]() 軸上方平面內的一點,以O、D、M、N為頂點的四邊形是菱形,求點N的坐標.
軸上方平面內的一點,以O、D、M、N為頂點的四邊形是菱形,求點N的坐標.

【答案】(1)![]() ;
;
(2)M(1, ![]() );
);
(3)當四邊形OMDN是菱形時,M(![]() ,
,![]() )N(
)N(![]() ,
,![]() )
)
【解析】分析:(1)首先在一次函數的解析式中令x=0,即可求得D的坐標,則OD的長度即可求得,OD=b,則E的坐標即可利用b表示出來,然后代入一次函數解析式即可得到關于b的方程,求得b的值;(2)首先求得四邊形OAED的面積,則△ODM的面積即可求得,設出M的橫坐標,根據三角形的面積公式即可求得M的橫坐標,進而求得M的坐標;(3)分成四邊形OMDN是菱形和四邊形OMND是菱形兩種情況進行討論,四邊形OMDN是菱形時,M是OD的中垂線與DE的交點,M關于OD的對稱點就是N;四邊形OMND是菱形,OM=OD,M在直角DE上,設出M的坐標,根據OM=OD即可求得M的坐標,則根據ON和DM的中點重合,即可求得N的坐標.
本題解析:(1)y=![]() x+b中,令x=0,解得y=b,則D的坐標是(0,b),OD=b,
x+b中,令x=0,解得y=b,則D的坐標是(0,b),OD=b,
∵OD=BE,
∴BE=b,則E的坐標是(3,4b),
把E的坐標代入y=![]() x+b得4b=2+b,
x+b得4b=2+b,
解得:b=3;
(2) ![]() ,
,
∵三角形ODM的面積與四邊形OAEM的面積之比為1:3,
∴![]() .
.
設M的橫坐標是a,則![]() ×3a=1.5,解得:a=1,
×3a=1.5,解得:a=1,
把x=a=1代入y=![]() x+3得y=
x+3得y=![]() ×
×![]() +3=
+3=![]() .
.
則M的坐標是(1, ![]() );
);
(3)當四邊形OMDN是菱形時,如圖(1),M的縱坐標是![]() ,把y=
,把y=![]() 代入y=
代入y=![]() x+3,得
x+3,得![]() x+3=
x+3=![]() ,解得:x=
,解得:x=![]() ,
,
則M的坐標是(![]() ,
,![]() ),
),
則N的坐標是(![]() ,
,![]() );
);
當四邊形OMND是菱形時,如圖(2)OM=OD=3,設M的橫坐標是m,則縱坐標是![]() m+3,則
m+3,則![]() ,
,
解得:m=![]() 或0(舍去).
或0(舍去).
則M的坐標是(![]() ,
,![]() ).
).
則DM的中點是(![]() ,
,![]() ).
).
則N的坐標是(![]() ,
,![]() ).
).
故N的坐標是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:
【題目】一個正方體的六個面上分別標有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一個數,各個面上所標數字都不相同,如圖是這個正方體的三種放置方法,三個正方體下底面所標數字分別是a,b,c,則a+b+c+abc= .

查看答案和解析>>
科目:初中數學 來源: 題型:
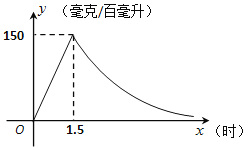
【題目】實驗數據顯示,一般成人喝半斤低度白酒后,1.5小時內其血液中酒精含量![]() (毫克/百毫升)與時間
(毫克/百毫升)與時間![]() (時)成正比例;1.5小時后(包括1.5小時)
(時)成正比例;1.5小時后(包括1.5小時)![]() 與
與![]() 成反比例.根據圖中提供的信息,解答下列問題:
成反比例.根據圖中提供的信息,解答下列問題:
(1)求一般成人喝半斤低度白酒后, ![]() 與
與![]() 之間的兩個函數關系式及相應的自變量
之間的兩個函數關系式及相應的自變量![]() 取值范圍;
取值范圍;
(2)依據人的生理數據顯示,當![]() ≥80時,肝部正被嚴重損傷,請問喝半斤低度白酒后,肝部被嚴重損傷持續多少小時?
≥80時,肝部正被嚴重損傷,請問喝半斤低度白酒后,肝部被嚴重損傷持續多少小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
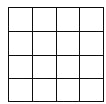
【題目】(1)如上圖,正方形網格中的每個小正方形邊長都是1,任意連接這些小正方形的頂點,可得到一些線段;請在圖中畫出AB=![]() ,CD=
,CD=![]() ,EF=
,EF=![]() 這樣的線段;
這樣的線段;
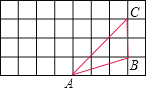
(2)如圖所示,在邊長為1的網格中作出△ABC繞點A按逆時針方向旋轉90°后的圖形△ABC;并計算對應點B和B之間的距離?
(3)如圖是由5個邊長為1的小正方形拼成的.
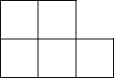
①將該圖形分成三塊(在圖中畫出),使由這三塊可拼成一個正方形;
②求出所拼成的正方形的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個工程隊共同承擔一項筑路任務,甲隊單獨施工完成此項任務比乙隊單獨施工完成此項任務多用10天,且甲隊單獨施工45天和乙隊單獨施工30天的工作量相同.
(1)甲、乙兩隊單獨完成此項任務各需多少天?
(2)若甲、乙兩隊共同工作了3天后,乙隊因設備檢修停止施工,由甲隊繼續施工,為了不影響工程進度,甲隊的工作效率提高到原來的2倍,要使甲隊總的工作量不少于乙隊的工作量的2倍,那么甲隊至少再單獨施工多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
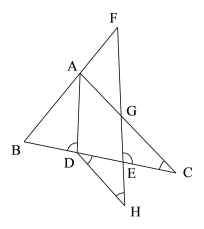
【題目】如圖,在△ABC中,AD平分∠BAC交BC于點D,點F在BA的延長線上,點E在線段CD上,EF與AC相交于點G,AD∥EF.
(1)求證:∠BDA+∠CEG=180°;
(2)若點H在FE的延長線上,且∠F=∠H,則∠EDH與∠C相等嗎,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李先生在2018年9月第14周星期五股市收盤時,以每股9元的價格買進某公司的股票1000股,在9月第3周的星期一至星期五,該股票每天收盤時每股的漲跌(單位:元)情況如下表:注:表中記錄的數據為每天收盤價格與前一天收盤價格的變化量,星期一的數據是與上星期五收盤價格的變化量.

(1)請你判斷在9月的第3周內,該股票價格收盤時,價格最高的是哪一天?
(2)在9月第3周內,求李先生購買的股票每股每天平均的收盤價格.(結果精確到百分位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖已知P為⊙O外一點,PA為⊙O的切線,B為⊙O上一點,且PA=PB,C為優弧 ![]() 上任意一點(不與A、B重合),連接OP、AB,AB與OP相交于點D,連接AC、BC.
上任意一點(不與A、B重合),連接OP、AB,AB與OP相交于點D,連接AC、BC.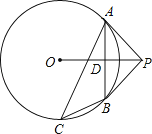
(1)求證:PB為⊙O的切線;
(2)若tan∠BCA= ![]() ,⊙O的半徑為
,⊙O的半徑為 ![]() ,求弦AB的長.
,求弦AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是由若干個小圓圈堆成的一個形如等邊三角形的圖案,最上面一層有一個圓圈,
以下各層均比上一層多一個圓圈,一共堆了n 層.將圖1倒置后與原圖1拼成圖2的形狀,這樣我們可以
算出圖1中所有圓圈的個數為1+2+3+…+n=![]() .
.

如果圖中的圓圈共有13層,請解決下列問題:
(1)我們自上往下,在每個圓圈中按圖3的方式填上一串連續的正整數1,2,3,4,……,則最底層最左
邊這個圓圈中的數是 ;
(2)我們自上往下,在每個圓圈中按圖4的方式填上一串連續的整數-23,-22,-21,-20,……,求
最底層最右邊圓圈內的數是_______;
(3)求圖4中所有圓圈中各數的絕對值之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com