
【題目】綜合與探究
如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且
,且![]() 點
點![]() 是
是![]() 的平分線與拋物線的交點.
的平分線與拋物線的交點.
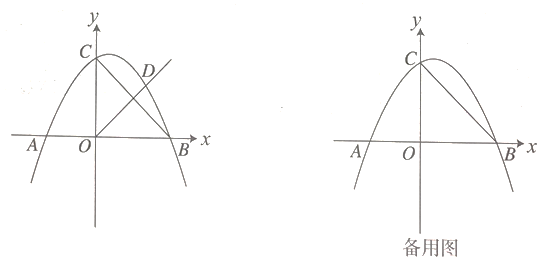
![]() 求拋物線的解析式及點
求拋物線的解析式及點![]() 的坐標;
的坐標;
![]() 點
點![]() 在平面直角坐標系內,且以
在平面直角坐標系內,且以![]() 點為頂點的四邊形是平行四邊形,請直接寫出滿足條件的點
點為頂點的四邊形是平行四邊形,請直接寫出滿足條件的點![]() 的坐標.
的坐標.
![]() 若點
若點![]() 是直線
是直線![]() 上方拋物線上的一個動點,且點
上方拋物線上的一個動點,且點![]() 的橫坐標為
的橫坐標為![]() 請寫出
請寫出![]() 的面積
的面積![]() 與
與![]() 之間的關系式,并求出
之間的關系式,并求出![]() 為何值時,
為何值時,![]() 的面積
的面積![]() 有最大值,最大值為多少.
有最大值,最大值為多少.
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]()
【解析】
(1)根據![]() ,可得
,可得![]() ,再利用待定系數法即可求得
,再利用待定系數法即可求得![]() ,再根據點
,再根據點![]() 是
是![]() 的平分線與拋物線的交點,可設
的平分線與拋物線的交點,可設![]() ,代入拋物線
,代入拋物線![]() ,即可求解.
,即可求解.
(2)分以OB、OD為鄰邊的平行四邊形、以OB、BD為鄰邊的平行四邊形、以DB、OD為鄰邊的平行四邊形三種情況 .
(3)作直線![]() 軸于點
軸于點![]() 交
交![]() 于點
于點![]() ,
,![]() 點坐標為
點坐標為![]() ,設直線
,設直線![]() 的解析式
的解析式![]() ,根據
,根據![]() ,可得直線
,可得直線![]() 解析式為
解析式為![]()
![]() ,
,![]() ,
,![]() 即可求解.
即可求解.
![]()
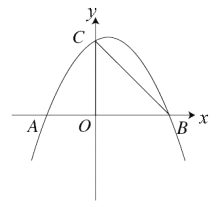
![]()
把![]() 兩點代入拋物線
兩點代入拋物線![]()
可得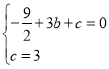
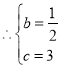
得拋物線解析式為![]()
![]() 點
點![]() 是
是![]() 的平分線與拋物線的交點,
的平分線與拋物線的交點,
![]() 設
設![]() ,代入拋物線
,代入拋物線![]()
得![]() (舍去,因為點
(舍去,因為點![]() 第一象限)
第一象限)
![]()
(2)
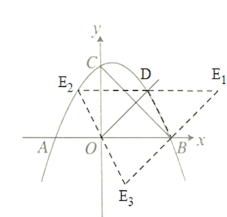
連接BD
若是以OB、OD為鄰邊的平行四邊形
則![]()
故只需把點D向右平移3個單位即得到點![]()
由(1)知D(2,2)
∴![]()
若是以OB、BD為鄰邊的平行四邊形
則![]()
故只需把點D向左平移3個單位即得到點![]()
∴![]()
若是以DB、OD為鄰邊的平行四邊形
則OD∥![]()
則只需把點D向下平移2個單位再向右平移1個單位即得到B,對應地只需把點O向下平移2個單位再向右平移1個單位即得到![]()
∴![]()
綜上所述,滿足條件的E點坐標為:![]() .
.
![]() 作直線
作直線![]() 軸于點
軸于點![]() 交
交![]() 于點
于點![]()
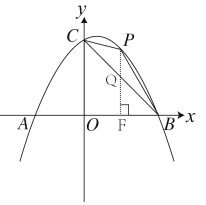
![]() 點坐標為
點坐標為![]()
設直線![]() 的解析式
的解析式![]() .
.
![]()
![]()
解得:![]()
可得直線![]() 解析式為
解析式為![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]()


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
【題目】“2018西安國際馬拉松”于2018年10月20日在陜西西安舉行,該賽事共有三項:![]() .“馬拉松”、
.“馬拉松”、![]() .“半程馬拉松”、
.“半程馬拉松”、![]() .“迷你馬拉松”小明和小剛有幸參與了該項賽事的志愿者服務工作,組委會隨機將志愿者分配到三個項目組.
.“迷你馬拉松”小明和小剛有幸參與了該項賽事的志愿者服務工作,組委會隨機將志愿者分配到三個項目組.
(1)小明被分配到“迷你馬拉松”項目組的概率為________.
(2)利用列表或樹狀圖求小明和小剛被分配到不同項目組的概率________.
查看答案和解析>>
科目:初中數學 來源: 題型:
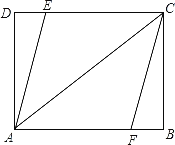
【題目】如圖,在矩形ABCD中,AB=16,AD=12,點E、F分別在邊CD、AB上.
(1)若DE=BF,求證:四邊形AFCE是平行四邊形;
(2)若四邊形AFCE是菱形,求菱形AFCE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,在等腰直角三角形中,底邊與一邊腰長比為![]() .如圖1,
.如圖1,![]() ,
,![]() ,則
,則![]() .
.

知識應用:
(1)如圖2,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() 三點共線,若
三點共線,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
知識外延:
(2)如圖3,正方形![]() 中,
中,![]() 和
和![]() 關于
關于![]() 對稱,
對稱,![]() 點的對應點為
點的對應點為![]() 點,
點,![]() 交
交![]() 的延長線于
的延長線于![]() 點,連接
點,連接![]() .
.
①求證:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,拋物線![]() 與
與![]() 軸交于B、C兩點(點B在點C右側),與
軸交于B、C兩點(點B在點C右側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,
,![]() .
.
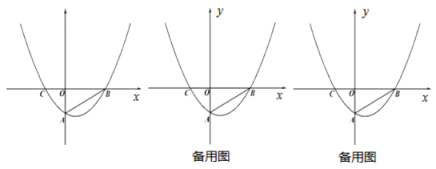
(1)求拋物線的解析式;
(2)點P在第二象限的拋物線上,連接PB交![]() 軸于D,取PB的中點E,過點E作
軸于D,取PB的中點E,過點E作![]() 軸于點H,連接DH,設點P的橫坐標為
軸于點H,連接DH,設點P的橫坐標為![]() .
.![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式(不要求寫出自變量
的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(3)在(2)的條件下,作![]() 軸于F,連接CP、CD,
軸于F,連接CP、CD,![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 交
交![]() 軸于點
軸于點![]() ,連接BF并延長交拋物線于點
,連接BF并延長交拋物線于點![]() .
.![]() ,在射線CS上取點Q.連接QF,
,在射線CS上取點Q.連接QF,![]() ,求直線
,求直線![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中有4個大小、質地完全相同的乒乓球,球面上都各標一個不小于-2的數,已知其中3個乒乓球上標的數分別是-2,2,4,所標的4個數的中位數是0.
(1)求這4個數的眾數;
(2)從這個口袋中隨機摸出1個球,求摸出的球面上的數是正數的概率;
(3)從這個口袋中隨機摸出1個球(不放回),再從余下的球中隨機摸出1個球,用列表法求兩次摸出的球面上的數之和為負數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
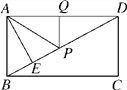
【題目】如圖,在矩形ABCD中,AD=6,AE⊥BD,垂足為E,DE=3BE,點P,Q分別在BD,AD 上,則AP+PQ的最小值為:
A. 2![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,
,![]() ,
,![]() .
.
(1)求此拋物線的解析式;
(2)若點![]() 是該拋物線第三象限的任意一點,求四邊形
是該拋物線第三象限的任意一點,求四邊形![]() 的最大面積;
的最大面積;
(3)若點![]() 在
在![]() 軸上,點
軸上,點![]() 為該拋物線的頂點,且
為該拋物線的頂點,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
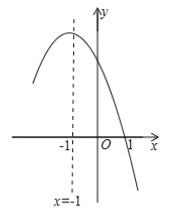
【題目】拋物線![]() 的對稱軸是直線
的對稱軸是直線![]() ,且過點
,且過點![]() ,頂點位于第二象限,其部分圖象如圖所示,給出以下判斷;①
,頂點位于第二象限,其部分圖象如圖所示,給出以下判斷;①![]() 且
且![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤直線
;⑤直線![]() 與拋物線
與拋物線![]() 兩個交點的橫坐標分別為
兩個交點的橫坐標分別為![]() ,則
,則![]() .其中結論正確是___________.
.其中結論正確是___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com