
【題目】如圖,△ABC中,AB = AC,AD、AE分別是∠BAC和∠BAC外角的平分線,![]() .
.

(1)求證:DA⊥AE;
(2)試判斷AB與DE是否相等?并證明你的結論.
【答案】(1)證明見解析;(2)AB=DE.證明見解析.
【解析】
試題(1)、根據角平分線的性質可得∠BAD=![]() ∠BAC,∠BAE=
∠BAC,∠BAE=![]() ∠BAF,根據平角的性質可以得出結論;(2)、根據等于三角形的三線合一定理說明∠ADB=90°,根據三個角是直角的四邊形為矩形得出ADBE為矩形,最后根據矩形的對角線的性質說明結論.
∠BAF,根據平角的性質可以得出結論;(2)、根據等于三角形的三線合一定理說明∠ADB=90°,根據三個角是直角的四邊形為矩形得出ADBE為矩形,最后根據矩形的對角線的性質說明結論.
試題解析:(1)、∵AD、AE分別為角平分線 ∴∠BAD=![]() ∠BAC,∠BAE=
∠BAC,∠BAE=![]() ∠BAF
∠BAF
∵∠BAC+∠BAF=180° ∴∠BAD+∠BAE=![]() (∠BAC+∠BAF)=90° ∴DA⊥AE
(∠BAC+∠BAF)=90° ∴DA⊥AE
、∵AB=AC AD為角平分線 ∴AD⊥BC 即∠ADB=90°
∵BE⊥AE ∴∠BEA=90° 又∵∠DAE=90° ∴四邊形ADBE為矩形 ∴AB=DE


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DEB中,已知AB=DE,還需添加兩個條件才能使△ABC≌△DEC,不能添加的一組條件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電器超市銷售每臺進價分別為200元、170元的A、B兩種型號的電風扇,下表是近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 3臺 | 5臺 | 1800元 |
第二周 | 4臺 | 10臺 | 3100元 |
(進價、售價均保持不變,利潤=銷售收入-進貨成本)
(1)求A、B兩種型號的電風扇的銷售單價;
(2)若超市準備用不多于5400元的金額再采購這兩種型號的電風扇共30臺,求A種型號的電風扇最多能采購多少臺?
(3)在(2)的條件下,超市銷售完這30臺電風扇能否實現利潤為1400元的目標?若能,請給出相應的采購方案;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一塊長、寬、高分別為6cm、4cm、3cm的長方體木塊,一只螞蟻要從長方體木塊的一個頂點A處,沿著長方體的表面到長方體上和A相對的頂點B處吃食物,那么它需要爬行的最短路徑的長是( )
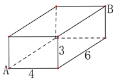
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 9cm
cm D. 9cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對非負實數x“四舍五入”到個位的值記為<x>,即當n為非負整數時,若![]() ,則<x>=n,如<0.46>=0,<3.67>=4。給出下列關于<x>的結論:
,則<x>=n,如<0.46>=0,<3.67>=4。給出下列關于<x>的結論:
①<1.493>=1;
②<2x>=2<x>;
③若![]() ,則實數x的取值范圍是
,則實數x的取值范圍是![]() ;
;
④當x≥0,m為非負整數時,有![]() ;
;
⑤![]() 。
。
其中,正確的結論有 (填寫所有正確的序號)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式,屬于二元一次方程的個數有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③![]() +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,點E是邊CD的中點,連接BE并延長,交AD延長線于點F,連接BD、CF.
(1)求證:△CEB≌△DEF;
(2)若AB=BF,試判斷四邊形BCFD的形狀,并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一些半徑相同的小圓按如圖所示的規律擺放:第1個圖形有6個小圓,第2個圖形有10個小圓,第3個圖形有16個小圓,第4個圖形有24個小圓,…,依次規律,第9個圖形圓的個數為( )
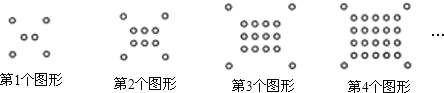
A.94B.85C.84D.76
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(數學經驗)三角形的中線的性質:三角形的中線等分三角形的面積.
(經驗發展)面積比和線段比的聯系:
(1)如圖1,M為△ABC的AB上一點,且BM=2AM.若△ABC的面積為a,若△CBM的面積為S,則S=_______(用含a的代數式表示).
(結論應用)(2)如圖2,已知△CDE的面積為1,![]() ,
,![]() ,求△ABC的面積.
,求△ABC的面積.
(遷移應用)(3)如圖3.在△ABC中,M是AB的三等分點(![]() ),N是BC的中點,若△ABC的面積是1,請直接寫出四邊形BMDN的面積為________.
),N是BC的中點,若△ABC的面積是1,請直接寫出四邊形BMDN的面積為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com