
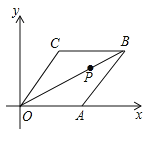
【題目】已知菱形![]() 在平面直角坐標系的位置如圖所示,頂點
在平面直角坐標系的位置如圖所示,頂點![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,![]() ,
,![]() ,點
,點![]() 是對角線
是對角線![]() 上的一個動點,點
上的一個動點,點![]() 的坐標為
的坐標為![]() ,則
,則![]() 最小值為( )
最小值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
連接AC,根據菱形的性質,點A、C關于直線OB對稱,連接AD與OB相交于點P,根據軸對稱確定最短路線問題,點P即為所求作的使CP+DP最小的點,根據菱形的對角線平分一組對角求出∠AOB=30°,然后求出OA的長度,根據點D的坐標求出OD,再利用勾股定理列式計算求出AD,從而得解.
解:如圖,連接AC,
∵四邊形OABC是菱形,
∴點A、C關于直線OB對稱,
連接AD與OB相交于點P,由軸對稱確定最短路線問題,點P即為所求作的使CP+DP最小的點,CP+DP的最小值為AD的長度,
∵∠COA=60°,
∴∠AOB=![]() ∠COA=30°,
∠COA=30°,
∴![]() ,
,
∵點D的坐標為(0,1),
∴OD=1,
由勾股定理得,AD=![]() .
.
故選:D.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④當﹣1<x<3時,y>0;其中正確的是( )
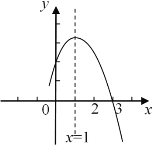
A.①②B.①②④C.②③④D.③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△OAB在平面直角坐標系中的位置如圖所示,將△ABO繞原點O逆時針旋轉90°得到△OA1B1.
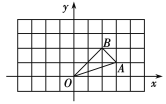
(1)畫出△OA1B1,并寫出點A1、B1的坐標;
(2)求△ABO繞原點O逆時針旋轉90°掃過的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出:將正m邊形(m≥3)不斷向外擴展,每擴展一個正m邊形每條邊上的點的個數(以下簡稱“點數”)就增加一個,則n個正m邊形的點數總共有多少個?
問題探究:為了解決上面的問題,我們將采取將一般問題特殊化的策略,先從簡單和具體的情形入手:
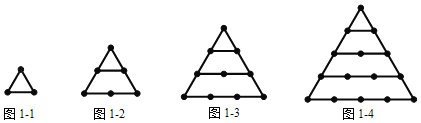
探究一:n個正三角形的點數總共有多少個?
如圖1﹣1,1個正三角形的點數總共有3個;如圖1﹣2,2個正三角形的點數總共有6個;如圖1﹣3,3個正三角形的點數總共有10個;…;n個正三角形的點數總共有 個.
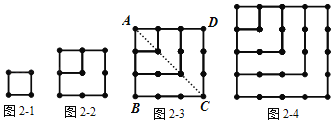
探究二:n個正四邊形的點數總共有多少個?
如圖2﹣1,1個正四邊形的點數總共有4個;如圖2﹣2,2個正四邊形的點數總共有9個;
如圖2﹣3,連接AC,得到兩個三角形△ABC和△ADC,這兩個三角形相同之處在于,BC邊與CD邊都有相同個數的點,即4個點,并且與BC、CD平行的邊上依次減少一個點直至頂點A,每個三角形都有10個點,兩個三角形就是2×10個點.因為這兩個三角形在AC上有4個點重合,所以3個正四邊形的點數總共有2×10﹣4=16(個).
如圖2﹣4,4個正四邊形的點數總共有 個;……n個正四邊形的點數總共有 個.
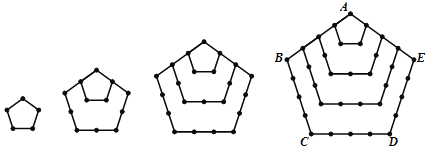
探究三:n個正五邊形的點數總共有多少個?
類比探究二的方法,求4個正五邊形的點數總共有多少個?并敘述你的探究過程.
n個正五邊形的點數總共有 個.
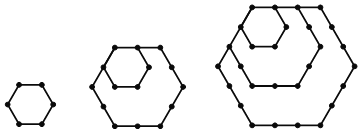
探究四:n個正六邊形的點數總共有 個.
問題解決:n個正m邊形的點數總共有 個.
實際應用:若99個正m邊形的點數總共有39700個,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
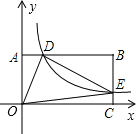
【題目】如圖,在以O為原點的直角坐標系中,矩形OABC的兩邊OC、OA分別在x軸、y軸的正半軸上,反比例函數y=![]() (x>0)的圖象與AB相交于點D.與BC相交于點E,且BD=3,AD=6,△ODE的面積為15,若動點P在x軸上,則PD+PE的最小值是_____.
(x>0)的圖象與AB相交于點D.與BC相交于點E,且BD=3,AD=6,△ODE的面積為15,若動點P在x軸上,則PD+PE的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(新洲區月考)如圖1,AB為半圓O的直徑,C為圓弧上一點,過點C的直線與AB的延長線交于點E,AD⊥CE于點D,AC平分∠DAB.
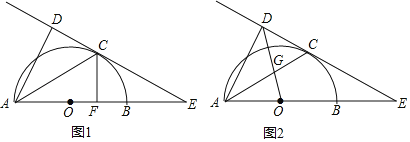
(1)求證:CE是⊙O的切線.
(2)若AB=6,B為OE的中點,CF⊥AB,垂足為點F,求CF的長;
(3)如圖2,連接OD交AC于點G,若![]() ,求sinE的值.
,求sinE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
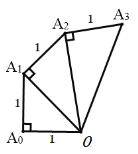
【題目】已知A0 A1= A1A2= A2A3…,圖中的螺旋形由一系列直角三角形組成,則第n個三角形的面積為_________,周長為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是⊙O的直徑,AB=10,![]() ,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=
,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結論中正確的個數是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結論中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】距離中考體考時間越來越近,年級想了解初三年級1512名學生周末在家體育鍛煉的情況,在初三年級隨機抽取了18名男生和18名女生,對他們周末在家的鍛煉時間進行了調查,并收集得到了以下數據(單位:分鐘)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
統計數據,并制作了如下統計表:
時間 |
|
|
|
|
男生 | 2 |
|
| 4 |
女生 | 1 | 5 | 9 | 3 |
分析數據:兩組數據的極差、平均數、中位數、眾數如表所示
極差 | 平均數 | 中位數 | 方差 | ||
男生 | 77 | 66.7 |
| 70 | 617.3 |
女生 |
| 69.7 | 70.5 |
| 547.2 |
(1)請將上面的表格補充完整:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)已知該年級男女生人數差不多,根據調查的數據,估計初三年級周末在家鍛煉的時間在90分鐘以上(不包含90分鐘)的同學約有多少人?
(3)體育老師看了表格數據后認為初三年級的女生周末鍛煉做得比男生好,請你結合統計數據,寫出兩條支持體育老師觀點的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com