【題目】觀察等式：
；
；
…，若設
，則用含
的式子表示
的結果是________．
【答案】
【解析】
由等式：2+22=23-2；2+22+23=24-2；2+22+23+24=25-2，得出規律：2+22+23+…+2n=2n+1-2，那么250+251+252+…+299+2100=(2+22+23+…+2100)-(2+22+23+…+249)，將規律代入計算即可．
∵2+22=23-2；
2+22+23=24-2；
2+22+23+24=25-2；
…
∴2+22+23+…+2n=2n+1-2，
∴250+251+252+…+299+2100
=(2+22+23+…+2100)-(2+22+23+…+249)
=(2101-2)-(250-2)
=2101-250，
∵250=a，
∴2101=(250)22=
，
∴原式=．
故答案為：．
科目：初中數學 來源： 題型：
【題目】新冠肺炎疫情爆發之后，全國許多省市對湖北各地進行了援助，廣州市某醫療隊備好醫療防護物資迅速援助武漢．第一批醫療隊員乘坐高鐵從廣州出發，2.5小時后，第二批醫療隊員乘坐飛機從廣州出發，兩批隊員剛好同時到達武漢．已知廣州到武漢的飛行距離為800千米，高鐵路程為飛行距離的
倍．
（1）求廣州到武漢的高鐵路程；
（2）若飛機速度與高鐵速度之比為5：2，求飛機和高鐵的速度．
查看答案和解析>>
科目：初中數學 來源： 題型：
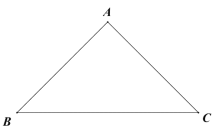
【題目】過三角形的任意兩個頂點畫一條弧，若弧上的所有點都在該三角形的內部或邊上，則稱該弧為三角形的“形內弧”．
（1）如圖，在等腰
中，
，
．
①在下圖中畫出一條的形內弧；
②在中，其形內弧的長度最長為______．
（2）在平面直角坐標系中，點
，
，
．點M為
形內弧所在圓的圓心．求點M縱坐標
的取值范圍；
（3）在平面直角坐標系中，點
，點G為x軸上一點．點P為
最長形內弧所在圓的圓心，求點P縱坐標
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
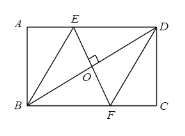
【題目】如圖，在矩形ABCD中，AB=3，做BD的垂直平分線E，F，分別與AD、BC交于點E、F，連接BE，DF，若EF=AE+FC，則邊BC的長為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
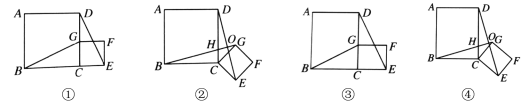
【題目】（1）在正方形ABCD中，G是CD邊上的一個動點（不與C、D重合），以CG為邊在正方形ABCD外作一個正方形CEFG，連結BG、DE，如圖①．直接寫出線段BG、DE的關系 ；
（2）將圖①中的正方形CEFG繞點C按順時針方向旋轉任意角度
，如圖②，試判斷（1）中的結論是否成立？若成立，直接寫出結論，若不成立，說明理由；
（3）將（1）中的正方形都改為矩形，如圖③，再將矩形CEFG繞點C按順時針方向旋轉任意角度，如圖④，若AB=a，BC=b；CE =ka，CG=kb，(
)試判斷（1）中的結論是否仍然成立？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們規定，以二次函數
的二次項系數
的2倍為一次項系數，一次項系數
為常數項構造的一次函數
叫做二次函數的“子函數”，反過來，二次函數叫做一次函數的“母函數”．
（1）若一次函數
是二次函數的“子函數”，且二次函數經過點
，求此二次函數的解析式．
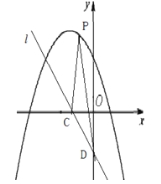
（2）如圖，已知二次函數
的“子函數”圖象直線
與
軸、
軸交于
、
兩點，點
是直線上方的拋物線上任意一點，求
的面積的最大值．
（3）已知二次函數
與它的“子函數”
的函數圖象有兩個交點
，
，且
，求
的值；
查看答案和解析>>
科目：初中數學 來源： 題型：
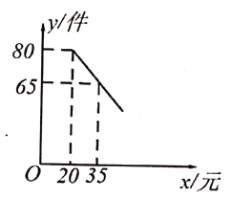
【題目】某超市購進一批成本為每件
元的商品，經調查發現，該商品每天的銷售量
(件)與銷售單價
(元)之間滿足一次函數關系，其圖象如圖所示．
（1）求該商品每天的銷售量與銷售單價之間的函數關系式；
（2）若超市按單價不低于成本價，且不高于
元銷售，則銷售單價定為多少，才能使銷售該商品每天獲得的利潤
(元)最大?
（3）若超市要使銷售該商品每天獲得的利潤為
元，則每天的銷售量應為多少件?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場計劃購進
，
兩種新型節能臺燈共120盞，這兩種臺燈的進價和售價如表所示：
價格 類型 | 進價（元/盞） | 售價（元/盞） |
| 40 | 55 |
| 60 | 80 |
（1）若商場恰好用完預計進貨款5500元，則應這購進兩種臺燈各多少盞？
（2）若商場規定型臺燈的進貨數量不超過型臺燈數量的3倍，應怎樣進貨才能使商場在銷售完這兩種臺燈時獲得的毛利潤最多？最多毛利潤為多少元？（毛利潤=銷售收入－進貨成本）．
查看答案和解析>>
科目：初中數學 來源： 題型：
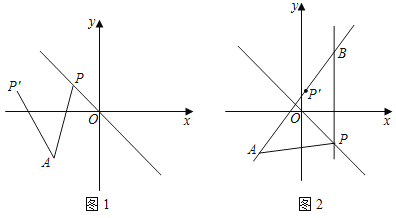
【題目】如圖1，點P(m，n)在一次函數y＝﹣x的圖象上，將點P繞點A(﹣
，﹣)逆時針旋轉45°，旋轉后的對應點為P′．
（1）當m＝0時，求點P′的坐標；
（2）試說明：不論m為何值，點P′的縱坐標始終不變；
（3）如圖2，過點P作x軸的垂線交直線AP′于點B，若直線PB與二次函數y＝﹣x2﹣x+2的圖象交于點Q，當m＞0時，試判斷點B是否一定在點Q的上方，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com