
【題目】已知:△ABC是三邊都不相等的三角形,點O和點P是這個三角形內部兩點.
(1)如圖①,如果點P是這個三角形三個內角平分線的交點,那么∠BPC和∠BAC有怎樣的數量關系?請說明理由;
(2)如圖②,如果點O是這個三角形三邊垂直平分線的交點,那么∠BOC和∠BAC有怎樣的數量關系?請說明理由;
(3)如圖③,如果點P(三角形三個內角平分線的交點),點O(三角形三邊垂直平分線的交點)同時在不等邊△ABC的內部,那么∠BPC和∠BOC有怎樣的數量關系?請直接回答.
【答案】(1)∠BPC=90°+![]() ∠BAC,理由見解析;(2)∠BOC=2∠BAC
∠BAC,理由見解析;(2)∠BOC=2∠BAC
,理由見解析;(3)4∠BPC-∠BOC=360°,理由見解析;
【解析】
(1)根據三角形角平分線的性質以及三角形內角和定理推導即可;
(2)根據三角形垂直平分線的性質以及三角形內角和定理推導即可;
(3)結合(1)(2)的結論∠BPC=90°+![]() ∠BAC、∠BOC=2∠BAC,通過等量代換即可.
∠BAC、∠BOC=2∠BAC,通過等量代換即可.
解:(1)∠BPC=90°+![]() ∠BAC
∠BAC
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=![]() ∠ABC,∠PCB=
∠ABC,∠PCB=![]() ∠ACB,
∠ACB,
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-(![]() ∠ABC+
∠ABC+![]() ∠ACB)
∠ACB)
=180°-![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°-![]() (180°-∠BAC)
(180°-∠BAC)
=90°+![]() ∠BAC;
∠BAC;
(2)∠BOC=2∠BAC
如圖,連接AO.
∵點O是這個三角形三邊垂直平分線的交點,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°-2∠OAB,∠AOC=180°-2∠OAC,
∴∠BOC=360°-(∠AOB+∠AOC)
=360°-(180°-2∠OAB+180°-2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC;
(3)4∠BPC-∠BOC=360°,
∵點P為三角形三個內角平分線的交點,
∴∠BPC=90°+![]() ∠BAC
∠BAC
由∠BAC=2∠BPC-180°
點O為三角形三邊垂直平分線的交點
∠BOC=2∠BAC,
∴∠BOC=2(2∠BPC-180°)=4∠BPC-360°,
即4∠BPC-∠BOC=360°.


科目:初中數學 來源: 題型:
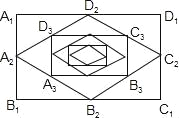
【題目】如圖:順次連接矩形A1B1C1D1四邊的中點得到四邊形A2B2C2D2,再順次連接四邊形A2B2C2D2四邊的中點得四邊形A3B3C3D3,…,按此規律得到四邊形AnBnCnDn.若矩形A1B1C1D1的面積為24,那么四邊形A2019B2019C2019D2019的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y=![]() 與一次函數y=-2x+m的圖象交于A、B兩點,AC⊥x軸于C, △AOC的面積為3.
與一次函數y=-2x+m的圖象交于A、B兩點,AC⊥x軸于C, △AOC的面積為3.
(1)根據這些條件,試確定反比例函數的解析式;
(2)根據這些條件,你能求出一次函數的關系式嗎?如果能請你求出來;如果不能,請你添加一個條件,求出一次函數的關系式.(注意:不能添加m的值);
(3)根據你所求出的一次函數的關系式,求出△AOD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() ,點
,點![]() 在該函數的圖象上,點
在該函數的圖象上,點![]() 到
到![]() 軸、
軸、![]() 軸的距離分別為
軸的距離分別為![]() 、
、![]() .設
.設![]() ,下列結論中:
,下列結論中:
①![]() 沒有最大值;②
沒有最大值;②![]() 沒有最小值;③
沒有最小值;③![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
④滿足![]() 的點
的點![]() 有四個.其中正確結論的個數有( )
有四個.其中正確結論的個數有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新華商場銷售某種冰箱,每臺進價為2500元,銷售價為2900元,平均每天能售出8臺;調查發現,當銷售價每降低50元,平均每天就能多售出4臺.商場要想使這種冰箱的銷售利潤平均每天達到5000元,每臺冰箱應該降價多少元?若設每臺冰箱降價x元,根據題意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() 與x、y軸分別交于A、B兩點,
與x、y軸分別交于A、B兩點,![]() 與x、y軸交于C、D兩點.
與x、y軸交于C、D兩點.
(1)求A、B、C、D的坐標(用含k、m的代數式表示);
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的前提下,若![]() 的面積為27,求m的值.
的面積為27,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 經過點
經過點![]() 和點
和點![]() ,交
,交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于
軸于![]() ,則:①
,則:①![]() ;②無論
;②無論![]() 取何值,此二次函數圖象與
取何值,此二次函數圖象與![]() 軸必有兩個交點,函數圖象截
軸必有兩個交點,函數圖象截![]() 軸所得的線段長度必大于
軸所得的線段長度必大于![]() ;③當函數在
;③當函數在![]() 時,
時,![]() 隨
隨![]() 的增大而減小;④當
的增大而減小;④當![]() 時,
時,![]() ;⑤若
;⑤若![]() ,則
,則![]() .以上說法正確的有( )
.以上說法正確的有( )
A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() 交于A、B兩點,且點A的橫坐標為
交于A、B兩點,且點A的橫坐標為![]() .
.
(1)求k的值;
(2)若雙曲線y=![]() 上點C的縱坐標為3,求△AOC的面積;
上點C的縱坐標為3,求△AOC的面積;
(3)在坐標軸上有一點M,在直線AB上有一點P,在雙曲線y=![]() 上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.
上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,李老師出示了如下框中的題目.
在等邊三角形ABC中,點E在AB上,點D在CB的延長線上,且ED=EC,如圖.試確定線段AE與DB的大小關系,并說明理由. |
|
小敏與同桌小聰討論后,進行了如下解答:
(1)特殊情況,探索結論
當點E為AB的中點時,如圖1,確定線段AE與的DB大小關系.請你直接寫出結論:
AE DB(填“>”,“<”或“=”).

圖1 圖2
(2)特例啟發,解答題目
解:題目中,AE與DB的大小關系是:AE DB(填“>”,“<”或“=”).
理由如下:如圖2,過點E作EF∥BC,交AC于點F.
(請你完成以下解答過程)
(3)拓展結論,設計新題
在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC.若△ABC的邊長為1,AE=2,求CD的長(請你直接寫出結果).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com