
【題目】如圖,![]() 為矩形
為矩形![]() 的對(duì)角線(xiàn),將邊
的對(duì)角線(xiàn),將邊![]() 沿
沿![]() 折疊,使點(diǎn)
折疊,使點(diǎn)![]() 落在
落在![]() 上的點(diǎn)
上的點(diǎn)![]() 處,將邊
處,將邊![]() 沿
沿![]() 折疊,使點(diǎn)
折疊,使點(diǎn)![]() 落在
落在![]() 上的點(diǎn)
上的點(diǎn)![]() 處.
處.

(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若![]() 求四邊形
求四邊形![]() 的面積及
的面積及![]() 與
與![]() 之間的距離.
之間的距離.
【答案】(1)證明見(jiàn)解析;(2)面積為30,距離為![]() .
.
【解析】
(1)根據(jù)矩形的性質(zhì)可得![]() 從而得出
從而得出![]() ,然后根據(jù)折疊的性質(zhì)可得
,然后根據(jù)折疊的性質(zhì)可得![]() ,從而證出
,從而證出![]() 然后根據(jù)平行四邊形的定義即可證出結(jié)論;
然后根據(jù)平行四邊形的定義即可證出結(jié)論;
(2)根據(jù)勾股定理即可求出BC,從而求出CM,設(shè)![]() ,然后利用勾股定理列出方程即可求出CE和BE,然后根據(jù)平行四邊形的面積公式即可求出面積,然后根據(jù)勾股定理求出AE,再根據(jù)平行四邊形的面積公式即可求出
,然后利用勾股定理列出方程即可求出CE和BE,然后根據(jù)平行四邊形的面積公式即可求出面積,然后根據(jù)勾股定理求出AE,再根據(jù)平行四邊形的面積公式即可求出![]() 與
與![]() 之間的距離.
之間的距離.
![]() 證明:
證明:![]() 四邊形
四邊形![]() 是矩形
是矩形
![]()
![]()
由折疊的性質(zhì)可得![]() ,
,
又![]()
![]()
![]()
![]() 四邊形
四邊形![]() 是平行四邊形.
是平行四邊形.
![]() 在
在![]() 中,
中,![]()
則根據(jù)勾股定理得:![]() .
.
![]()
![]() .
.
設(shè)![]() ,則
,則![]()
在![]() 中,利用勾股定理可得
中,利用勾股定理可得![]()
即![]() ,
,
解得![]()
∴CE=5,BE=3
故四邊形![]() 的面積
的面積![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
設(shè)![]() 與
與![]() 之間的距離為
之間的距離為![]()
則![]() ,
,
即![]() ,
,
![]()


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優(yōu)沖刺100分系列答案
全優(yōu)沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地下車(chē)庫(kù)出口處安裝了“兩段式欄桿”,如圖1所示,點(diǎn)A是欄桿轉(zhuǎn)動(dòng)的支點(diǎn),點(diǎn)E是欄桿兩段的聯(lián)結(jié)點(diǎn).當(dāng)車(chē)輛經(jīng)過(guò)時(shí),欄桿AEF最多只能升起到如圖2所示的位置,其示意圖如圖3所示(欄桿寬度忽略不計(jì)),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么適合該地下車(chē)庫(kù)的車(chē)輛限高標(biāo)志牌為( )(參考數(shù)據(jù):sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知一個(gè)直角三角形的一邊長(zhǎng)等于另一邊長(zhǎng)的2倍,那么這個(gè)直角三角形中較小銳角的正切值為
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】請(qǐng)完成以下問(wèn)題: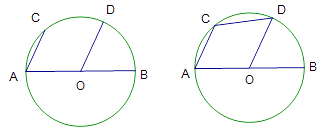
圖1 圖2
(1)如圖1, ![]() ,弦
,弦 ![]() 與半徑
與半徑 ![]() 平行,求證:
平行,求證: ![]() 是⊙
是⊙ ![]() 的直徑;
的直徑;
(2)如圖2, ![]() 是⊙
是⊙ ![]() 的直徑,弦
的直徑,弦 ![]() 與半徑
與半徑 ![]() 平行.已知圓的半徑為
平行.已知圓的半徑為 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 與
與 ![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 方向以
方向以![]() 的速度向點(diǎn)
的速度向點(diǎn)![]() 勻速運(yùn)動(dòng),同時(shí)點(diǎn)
勻速運(yùn)動(dòng),同時(shí)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 方向以
方向以![]() 的速度向點(diǎn)
的速度向點(diǎn)![]() 勻速運(yùn)動(dòng),當(dāng)其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng).設(shè)點(diǎn)
勻速運(yùn)動(dòng),當(dāng)其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng).設(shè)點(diǎn)![]() 運(yùn)動(dòng)的時(shí)間是
運(yùn)動(dòng)的時(shí)間是![]() .過(guò)點(diǎn)
.過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() 連結(jié)
連結(jié)![]()

(1)求證:![]() ;
;
(2)四邊形![]() 能夠成為菱形嗎?如果能,求出相應(yīng)的
能夠成為菱形嗎?如果能,求出相應(yīng)的![]() 值,如果不能,說(shuō)明理由;
值,如果不能,說(shuō)明理由;
(3)當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 為直角三角形?請(qǐng)說(shuō)明理由.
為直角三角形?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在⊙O中,AB是⊙O的直徑,AB=10,![]() ,點(diǎn)E是點(diǎn)D關(guān)于AB的對(duì)稱(chēng)點(diǎn),M是AB上的一動(dòng)點(diǎn),下列結(jié)論:①∠BOE=60°;②∠CED=
,點(diǎn)E是點(diǎn)D關(guān)于AB的對(duì)稱(chēng)點(diǎn),M是AB上的一動(dòng)點(diǎn),下列結(jié)論:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結(jié)論中正確的個(gè)數(shù)是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結(jié)論中正確的個(gè)數(shù)是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】完成下面的證明過(guò)程:
如圖所示,直線(xiàn)AD與AB,CD分別相交于點(diǎn)A,D,與EC,BF分別相交于點(diǎn)H,G,已知∠1=∠2,∠B=∠C.
求證:∠A=∠D.
證明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com