
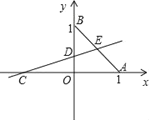
【題目】已知:如圖,平面直角坐標系xOy中,B(0,1),OB=OC=OA,A、C分別在x軸的正負半軸上.過點C的直線繞點C旋轉,交y軸于點D,交線段AB于點E.
(1)求∠OAB的度數及直線AB的解析式;
(2)若△OCD與△BDE的面積相等,求點D的坐標.
【答案】(1)45°,y=﹣x+1;(2)(0,![]() ).
).
【解析】
(1)根據A、B的坐標和三角形的內角和定理求出∠OAB的度數即可;設直線AB的解析式為y=kx+b,把A、B的坐標代入得出方程組,求出方程組的解即可;
(2)推出三角形AOB和三角形ACE的面積相等,根據面積公式求出E的縱坐標,代入直線AB的解析式,求出E的橫坐標,設直線CE的解析式是:y=mx+n,利用待定系數法求出直線EC的解析式,進而即可求得點D的坐標.
解:(1)∵OB=OC=OA,∠AOB=90°,
∴∠OAB=45°;
∵B(0,1),
∴A(1,0),
設直線AB的解析式為y=kx+b.
∴![]()
解得,
![]()
∴直線AB的解析式為y=﹣x+1;
(2)∵S△COD=S△BDE,
∴S△COD+S四邊形AODE=S△BDE+S四邊形AODE,
即S△ACE=S△AOB,
∵點E在線段AB上,
∴點E在第一象限,且yE>0,
∴![]()
∴![]()
![]()
把y![]() 代入直線AB的解析式得:
代入直線AB的解析式得:![]()
∴![]()
設直線CE的解析式是:y=mx+n,
∵![]() 代入得:
代入得: 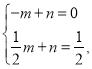
解得:![]()
∴直線CE的解析式為![]()
令x=0,則![]()
∴D的坐標為![]()


科目:初中數學 來源: 題型:
【題目】目前“微信”、“支付寶”、“共享單車”和“網購”給我們帶來了很多便利,初二數學小組在校內對“你最認可的四大新生事物”進行了調查,隨機調查了![]() 人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.
人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.

(1)根據圖中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)請你幫助他們將這兩個統計圖補全;
(3)根據抽樣調查的結果,請估算全校2000名學生種,大約有多少人最認可“微信”這一新生事物?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是小強洗漱時的側面示意圖,洗漱臺(矩形ABCD)靠墻擺放,高AD=80cm,寬AB=48cm,小強身高166cm,下半身FG=100cm,洗漱時下半身與地面成80°(∠FGK=80°),身體前傾成125°(∠EFG=125°),腳與洗漱臺距離GC=15cm(點D,C,G,K在同一直線上).
(1)此時小強頭部E點與地面DK相距多少?
(2)小強希望他的頭部E恰好在洗漱盆AB的中點O的正上方,他應向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,結果精確到0.1cm)
≈1.41,結果精確到0.1cm)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學藝術節期間,學校向學生征集書畫作品,楊老師從全校30個班中隨機抽取了4個班(用A,B,C,D表示),對征集到的作品的數量進行了分析統計,制作了兩幅不完整的統計圖.

請根據以上信息,回答下列問題:
(1)楊老師采用的調查方式是 (填“普查”或“抽樣調查”);
(2)請你將條形統計圖補充完整,并估計全校共征集多少件作品?
(3)如果全校征集的作品中有5件獲得一等獎,其中有3名作者是男生,2名作者是女生,現要在獲得一等獎的作者中選取兩人參加表彰座談會,請你用列表或樹狀圖的方法,求恰好選取的兩名學生性別相同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點 A、B 在數軸上分別表示有理數 a、b,A、B 兩點之間的距離表示為 AB, 在數軸上 A、B 兩點之間的距離 AB=|a﹣b|.
![]()
請用上面的知識解答下面的問題:
(1)數軸上表示 1 和 5 的兩點之間的距離是 ,數軸上表示﹣2 和﹣4 的 兩點之間的距離是 ,數軸上表示 1 和﹣3 的兩點之間的距離是 ;
(2)數軸上表示 x 和﹣1 的兩點 A 和 B 之間的距離是 ,如果|AB|=2, 那么 x 為 ;
(3)|x+1|+|x﹣2|取最小值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖已知數軸上點![]() 、
、![]() 分別表示
分別表示![]() 、
、![]() ,且
,且![]() 與
與![]() 互為相反數,
互為相反數,![]() 為原點.
為原點.
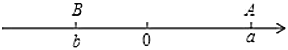
(1)![]() ______,
______,![]() ______;
______;
(2)將數軸沿某個點折疊,使得點![]() 與表示-10的點重合,則此時與點
與表示-10的點重合,則此時與點![]() 重合的點所表示的數為______;
重合的點所表示的數為______;
(3)若點![]() 、
、![]() 分別從點
分別從點![]() 、
、![]() 同時出發,點
同時出發,點![]() 以每秒1個單位長度的速度沿數軸向左勻速運動,點
以每秒1個單位長度的速度沿數軸向左勻速運動,點![]() 以每秒2個單位長度的速度沿數軸向右勻速運動,
以每秒2個單位長度的速度沿數軸向右勻速運動,![]() 到點
到點![]() 后立刻原速返回,設運動時間為
后立刻原速返回,設運動時間為![]() 秒.
秒.
①點![]() 表示的數是______(用含
表示的數是______(用含![]() 的代數式表示);
的代數式表示);
②求![]() 為何值時,
為何值時,![]() ;
;
③求![]() 為何值時,點
為何值時,點![]() 與
與![]() 相距3個單位長度.
相距3個單位長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某勘測隊在一條近似筆直的河流l兩邊勘測(河寬忽略不計),共設置了A,B,C三個勘測點.
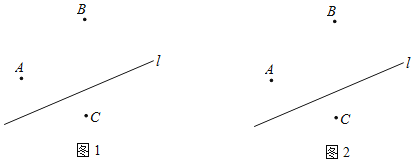
(1)若勘測隊在A點建一水池,現將河水引入到水池A中,則在河岸的什么位置開溝,才能使水溝的長度最短?請在圖1中畫出圖形;你畫圖的依據是 .
(2)若勘測隊在河岸某處開溝,使得該處到勘測點B,C所挖水溝的長度之和最短,請在圖2中畫出圖形;你畫圖的依據是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,與
,與![]() 互為余角,與
互為余角,與![]() 互為補角,
互為補角,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,

(1)如圖,當![]() 時,求
時,求![]() 的度數;
的度數;
(2)在(1)的條件下,請你補全圖形,并求![]() 的度數;
的度數;
(3)當![]() 為大于
為大于![]() 的銳角,且
的銳角,且![]() 與
與![]() 有重合部分時,請求出
有重合部分時,請求出![]() 的度數.(寫出說理過程,用含
的度數.(寫出說理過程,用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com