
【題目】如圖,有一平行四邊形ABCD與一正方形CEFG,其中E點在AD上.若∠ECD=35°,∠AEF=15°,則∠B的度數為何?( ) 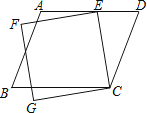
A.50
B.55
C.70
D.75
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
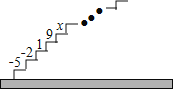
【題目】如圖,階梯圖的每個臺階上都標著一個數,從下到上的第1個至第4個臺階上依次標著﹣5,﹣2,1,9,且任意相鄰四個臺階上數的和都相等.
嘗試 (1)求前4個臺階上數的和是多少?
(2)求第5個臺階上的數x是多少?
應用 求從下到上前31個臺階上數的和.
發現 試用含k(k為正整數)的式子表示出數“1”所在的臺階數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,那么下列判斷不正確的是( ) 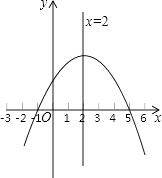
A.ac<0
B.a﹣b+c>0
C.b=﹣4a
D.關于x的方程ax2+bx+c=0的根是x1=﹣1,x2=5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=2x2﹣x﹣3.
(1)求函數圖象的頂點坐標,與坐標軸交點坐標,并畫出函數大致圖象; 
(2)根據圖象直接回答:當x為何值時,y<0?當x為何值時y>﹣3?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們學習了勾股定理后,都知道“勾三、股四、弦五”.
觀察:3,4,5;5,12,13;7,24,25;9,40,41;……發現這些勾股數的勾都是奇數,且從3起就沒有間斷過.
(1)請你根據上述的規律寫出下一組勾股數:_______________________;
(2)若第一個數用字母n(n為奇數,且n≥3)表示,則后兩個數用含n的代數式表示分別為___________________。
查看答案和解析>>
科目:初中數學 來源: 題型:
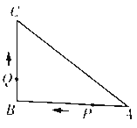
【題目】如圖,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC邊上的兩個動點,點P從點A開始沿A→B方向運動,且速度為1 cm,點Q從點B開始沿B→C方向運動,且速度為2 cm/s,它們同時出發,設運動的時間為t s.
(1)運動幾秒時,△APC是等腰三角形?
(2)當點Q在邊CA上運動時,求能使△BCQ成為等腰三角形的運動時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上有A、B兩個點.
(1)如圖1,若AB=a,M是AB的中點,C為線段AB上的一點,且![]() ,則AC= ,CB= ,MC= (用含a的代數式表示);
,則AC= ,CB= ,MC= (用含a的代數式表示);
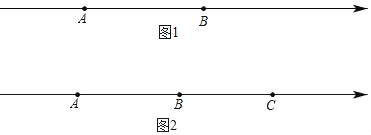
(2)如圖2,若A、B、C三點對應的數分別為﹣40,﹣10,20.
①當A、C兩點同時向左運動,同時B點向右運動,已知點A、B、C的速度分別為8個單位長度/秒、4個單位長度/秒、2個單位長度/秒,點M為線段AB的中點,點N為線段BC的中點,在B、C相遇前,在運動多少秒時恰好滿足:MB=3BN.
②現有動點P、Q都從C點出發,點P以每秒1個單位長度的速度向終點A移動;當點P移動到B點時,點Q才從C點出發,并以每秒3個單位長度的速度向左移動,且當點P到達A點時,點Q也停止移動(若設點P的運動時間為t).當PQ兩點間的距離恰為18個單位時,求滿足條件的時間t值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)小慧和小聰沿圖1中的景區公路游覽.小慧乘坐車速為30km/h的電動汽車,早上7:00從賓館出發,游玩后中午12:00回到賓館.小聰騎車從飛瀑出發前往賓館,速度為20km/h,途中遇見小慧時,小慧恰好游完一景點后乘車前往下一景點.上午10:00小聰到達賓館.圖2中的圖象分別表示兩人離賓館的路程s(km)與時間t(h)的函數關系.試結合圖中信息回答:

(1)小聰上午幾點鐘從飛瀑出發?
(2)試求線段AB、GH的交點B的坐標,并說明它的實際意義.
(3)如果小聰到達賓館后,立即以30km/h的速度按原路返回,那么返回途中他幾點鐘遇見小慧?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著私家車擁有量的增加,停車問題已經給人們的生活帶來了很多不便.為了緩解停車矛盾,某小區開發商欲投資16萬元,建造若干個停車位,考慮到實際因素,計劃露天車位的數量不少于室內車位的2倍,但不超過室內車位的3倍.據測算,建造費用及年租金如下表:
類別 | 室內車位 | 露天車位 |
建造費用(元/個) | 5 000 | 1 000 |
年租金(元/個) | 2 000 | 800 |
(1)該開發商有哪幾種符合題意的建造方案?寫出解答過程.
(2)若按表中的價格將兩種車位全部出租,哪種方案獲得的年租金最多?并求出此種方案的年租金.(不考慮其他費用)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com