
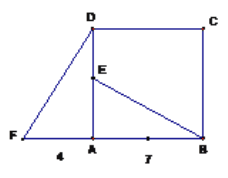
【題目】四邊形ABCD是正方形,△ADF旋轉一定角度后得到△ABE,如圖所示,如果AF=4,AB=7.
(1)旋轉中心是點 ,旋轉了 度,DE的長度是 ;
(2)BE與DF的關系如何? 請說明理由.(提示:延長BE交DF于點G)
【答案】(1)A;90;3;(2)BE⊥DF.
【解析】試題分析:(1)由△ADF繞點A順時針旋轉90度得到△ABE可知AE=AF=4,AD=AB=7,從而得出DE的長;
(2)根據旋轉的性質得出∠F=∠AEB=∠DEG,再根據∠F+∠ADF=90°可得∠DEG+∠ADF=90°,即可得答案.
試題解析:解:(1)根據題意可知,△ADF繞點A順時針旋轉90度得到△ABE,∴AE=AF=4,AD=AB=7,∴DE=AD﹣AE=3;
(2)BE⊥DF.理由如下:
如圖,延長BE交DF于點G.由旋轉的性質可得:∠AEB=∠F,又∵∠AEB=∠DEG,∴∠F=∠DEG,∵∠F+∠ADF=90°,∴∠DEG+∠ADF=90°,∴∠AGE=90°,即BE⊥DF.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某商場出售一批進價為2元的賀卡,在市場營銷中發現此商品的日銷售單價x(元)與日銷售量y(個)之間有如下關系:
日銷售單價x(元) | 3 | 4 | 5 | 6 |
日銷售量y(個) | 20 | 15 | 12 | 10 |
(1)猜測并確定y與x之間的函數關系式,并畫出圖象;
(2)設經營此賀卡的銷售利潤為W元,求出W與x之間的函數關系式,
(3)若物價局規定此賀卡的售價最高不能超過10元/個,請你求出當日銷售單價x定為多少時,才能獲得最大日銷售利潤?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒肺炎的防護知識,并鼓勵社區居民在線參與作答《2020年新型冠狀病毒防治全國統一考試(全國卷)》試卷,社區管理員隨機從甲、乙兩個小區各抽取20名人員的答卷成績,并對他們的成績(單位:分)進行統計、分析,過程如下:
收集數據
甲小區:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小區:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理數據
成績x(分) | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲小區 | 2 | 5 | a | b |
乙小區 | 3 | 7 | 5 | 5 |
分析數據
統計量 | 平均數 | 中位數 | 眾數 |
甲小區 | 85.75 | 87.5 | c |
乙小區 | 83.5 | d | 80 |
應用數據
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小區共有800人參與答卷,請估計甲小區成績大于90分的人數;
(3)社區管理員看完統計數據,認為甲小區對新型冠狀病毒肺炎防護知識掌握更好,請你寫出社區管理員的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中正確的是( )
A.在直角三角形中,兩條邊的平方和等于第三邊的平方
B.如果一個三角形兩邊的平方差等于第三邊的平方,那么這個三角形是直角三角形
C.在△ABC中,∠A,∠B,∠C的對邊分別為a,b,c,若a2+b2=c2,則∠A=90°
D.在△ABC中,若a=3,b=4,則c=5
查看答案和解析>>
科目:初中數學 來源: 題型:
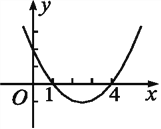
【題目】已知二次函數y=ax2-5x+c的圖象如圖所示.
(1)試求該二次函數的解析式和它的圖象的頂點坐標;
(2)觀察圖象回答,x何值時y的值大于0?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,二次函數y=-2x2+4x+m的圖象與x軸的一個交點為A(3,0),另一個交點為B,且與y軸交于點C.
(1)求m的值及點B的坐標;
(2)求△ABC的面積;
(3)該二次函數圖象上有一點D(x,y),使S△ABD=S△ABC,請求出D點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,∠ACB=90°,BC=2,AC=4,點D在射線BC上,以點D為圓心,BD為半徑畫弧交邊AB于點E,過點E作EF⊥AB交邊AC于點F,射線ED交射線AC于點G.
(1)求證:△EFG∽△AEG;
(2)設FG=x,△EFG的面積為y,求y關于x的函數解析式并寫出定義域;
(3)聯結DF,當△EFD是等腰三角形時,請直接寫出FG的長度.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據要求作圖.
(1)如圖1,平行四邊形ABCD,點E,F分別在邊AD,BC上,且AE=CF,連接EF.請你只用無刻度直尺畫出線段EF的中點O.(保留畫圖痕跡,不必說明理由).
(2)如圖2,平行四邊形ABCD,點E在邊AB上,請你只用無刻度直尺在邊CD上找一點F,使得四邊形AECF為平行四邊形,并說明理由.(注意:無刻度直尺只能過點畫線段或直線或射線).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com