
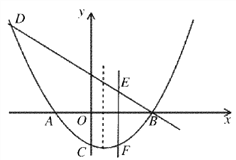
【題目】如圖,已知拋物線![]() (k為常數,且k>0)與x軸的交點為A、B,與y軸的交點為C,經過點B的直線
(k為常數,且k>0)與x軸的交點為A、B,與y軸的交點為C,經過點B的直線![]() 與拋物線的另一個交點為D.
與拋物線的另一個交點為D.
(1)若點D的橫坐標為x= -4,求這個一次函數與拋物線的解析式;
(2)若直線m平行于該拋物線的對稱軸,并且可以在線段AB間左右移動,它與直線BD和拋物線分別交于點E、F,求當m移動到什么位置時,EF的值最大,最大值是多少?
(3)問原拋物線在第一象限是否存在點P,使得△APB∽△ABC?若存在,請求出這時k的值;若不存在,請說明理由.
【答案】(1) ![]() (2) 最大值是4(3)存在
(2) 最大值是4(3)存在
【解析】分析:(1)先解方程k(x+2)(x﹣4)=0可得A(﹣2,0),B(4,0),再把B點坐標代入y=﹣![]() x+b中求出得b=2,則可得到一次函數解析式為y=﹣
x+b中求出得b=2,則可得到一次函數解析式為y=﹣![]() x+2,接著利用一次函數解析式確定D點坐標,然后把D點坐標代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得拋物線解析式;
x+2,接著利用一次函數解析式確定D點坐標,然后把D點坐標代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得拋物線解析式;
(2)利用二次函數和一次函數圖象上點的坐標特征,可設F(t,![]() t2﹣
t2﹣![]() t﹣2),則E(t,﹣
t﹣2),則E(t,﹣![]() t+2),﹣2≤t≤4,于是得到EF=﹣
t+2),﹣2≤t≤4,于是得到EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,然后根據二次函數的性質求解;
t2+4,然后根據二次函數的性質求解;
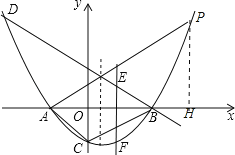
(3)作PH⊥x軸于H,如圖,先表示出C點坐標為(0,﹣8k),設P[n,k(n+2)(n﹣4)],根據相似三角形的判定方法,當∠PAB=∠CAB,AP:AB=AB:AC時,△APB∽△ABC;再根據正切定義.在Rt△APH中有tan∠PAH=![]() .在Rt△OAC中有tan∠OAC=
.在Rt△OAC中有tan∠OAC=![]() =4k,則
=4k,則![]() =4k,解得n=8,于是得到P(8,40k),接著利用勾股定理計算出AP=10
=4k,解得n=8,于是得到P(8,40k),接著利用勾股定理計算出AP=10![]() ,AC=2
,AC=2![]() ,然后利用AP:AB=AB:AC得到10
,然后利用AP:AB=AB:AC得到10![]() 2
2=62,解得k1=
![]() ,k2=﹣
,k2=﹣![]() (舍去),于是可確定P點坐標.
(舍去),于是可確定P點坐標.
詳解:(1)當y=0時,k(x+2)(x﹣4)=0,解得:x1=﹣2,x2=4,則A(﹣2,0),B(4,0),把B(4,0)代入y=﹣![]() x+b得:﹣2+b=0,解得:b=2,所以一次函數解析式為y=﹣
x+b得:﹣2+b=0,解得:b=2,所以一次函數解析式為y=﹣![]() x+2,當x=﹣4時,y=﹣
x+2,當x=﹣4時,y=﹣![]() x+2=4,則D點坐標為(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=
x+2=4,則D點坐標為(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=![]() ,所以拋物線解析式為y=
,所以拋物線解析式為y=![]() (x+2)(x﹣4),即y=
(x+2)(x﹣4),即y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)設F(t,![]() t2﹣
t2﹣![]() t﹣2),則E(t,﹣
t﹣2),則E(t,﹣![]() t+2),﹣2≤t≤4,所以EF=﹣
t+2),﹣2≤t≤4,所以EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,所以當t=0時,EF最大,最大值為4,即當直線m移動到與y軸重合的位置時,EF的值最大,最大值是4;
t2+4,所以當t=0時,EF最大,最大值為4,即當直線m移動到與y軸重合的位置時,EF的值最大,最大值是4;
(3)存在.
作PH⊥x軸于H,如圖,當x=0時,y=k(x+2)(x﹣4)=﹣8k,則C(0,﹣8k),設P[n,k(n+2)(n﹣4)],當∠PAB=∠CAB,AP:AB=AB:AC時,△APB∽△ABC;
在Rt△APH中,tan∠PAH=![]() .在Rt△OAC中,tan∠OAC=
.在Rt△OAC中,tan∠OAC=![]() =4k,∴
=4k,∴![]() =4k,解得:n=8,則P(8,40k),∴AP=
=4k,解得:n=8,則P(8,40k),∴AP=![]() =
=![]() =10
=10![]() ,而AC=
,而AC=![]() =
=![]() =2
=2![]() .∵AP:AB=AB:AC,∴APAC=AB2,即10
.∵AP:AB=AB:AC,∴APAC=AB2,即10![]() 2
2![]() =62,∴5(16k2+1)=9,解得:k1=
=62,∴5(16k2+1)=9,解得:k1=![]() ,k2=﹣
,k2=﹣![]() (舍去),∴k=4
(舍去),∴k=4![]() ,P點坐標為(8,4
,P點坐標為(8,4![]() ).
).


科目:初中數學 來源: 題型:
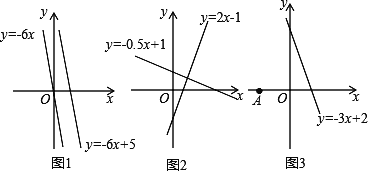
【題目】材料一:如圖1,由課本91頁例2畫函數y=﹣6x與y=﹣6x+5可知,直線y=﹣6x+5可以由直線y=﹣6x向上平移5個單位長度得到由此我們得到正確的結論一:在直線L1:y=K1x+b1與直線L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反過來,也成立.
材料二:如圖2,由課本92頁例3畫函數y=2x﹣1與y=﹣0.5x+1可知,利用所學知識一定能證出這兩條直線是互相垂直的.由此我們得到正確的結論二:在直線L1:y=k1x+b1 與L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反過來,也成立
應用舉例
已知直線y=﹣![]() x+5與直線y=kx+2互相垂直,則﹣
x+5與直線y=kx+2互相垂直,則﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解決問題
(1)請寫出一條直線解析式______,使它與直線y=x﹣3平行.
(2)如圖3,點A坐標為(﹣1,0),點P是直線y=﹣3x+2上一動點,當點P運動到何位置時,線段PA的長度最小?并求出此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一張長方形紙片,![]() (
(![]() ).將這張紙片沿著過點
).將這張紙片沿著過點![]() 的折痕翻折,使點
的折痕翻折,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() ,折痕交
,折痕交![]() 于點
于點![]() ,將折疊后的紙片再次沿著另一條過點
,將折疊后的紙片再次沿著另一條過點![]() 的折痕翻折,點
的折痕翻折,點![]() 恰好與點
恰好與點![]() 重合,此時折痕交
重合,此時折痕交![]() 于點
于點![]() .
.
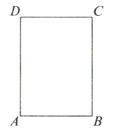
(1)在圖中確定點![]() 、點
、點![]() 和點
和點![]() 的位置;
的位置;
(2)聯結![]() ,則
,則![]() ______
______![]() ;
;
(3)用含有![]() 的代數式表示線段
的代數式表示線段![]() 的長.(注:直角三角形中,兩直角邊的平方的和等于斜邊的平方)
的長.(注:直角三角形中,兩直角邊的平方的和等于斜邊的平方)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知n邊形的內角和θ=(n﹣2)×180°.
(1)甲同學說,θ能取900°;而乙同學說,θ也能取800°.甲、乙的說法對嗎?若對,求出邊數n.若不對,說明理由;
(2)若n邊形變為(n+x)邊形,發現內角和增加了540°,用列方程的方法確定x.
查看答案和解析>>
科目:初中數學 來源: 題型:
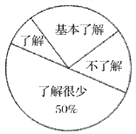
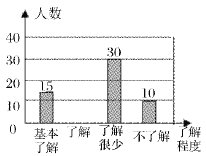
【題目】“食品安全”受到全社會的廣泛關注,我市某中學對部分學生就食品安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面的兩幅尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題:
(1)接受問卷調查的學生共有_________人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為_________度;
(2)請補全條形統計圖;
(3)若該中學共有學生900人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數;
扇形統計圖 條形統計圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩輛汽車同時從相距330千米的甲、乙兩地相向而行,s(千米)表示汽車與甲地的距離,t(分)表示汽車行駛的時間,如圖,L1,L2分別表示兩輛汽車的s與t的關系.
(1)L1表示哪輛汽車到甲地的距離與行駛時間的關系?
(2)汽車B的速度是多少?
(3)求L1,L2分別表示的兩輛汽車的s與t的關系式.
(4)2小時后,兩車相距多少千米?
(5)行駛多長時間后,A、B兩車相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
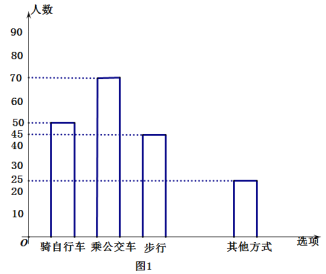
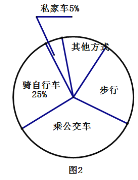
【題目】綠色出行是相對環保的出行方式,通過碳減排和碳中和實現環境資源的可持續利用和交通可持續發展.汽車工業的發展為人類帶來了快捷和方便,但同時,汽車的發展也引起了能源的消耗和空氣的污染.并且已成為全國各大城市的第一大污染源。實驗中學為了解全校學生的交通方式,責成該校七年級(1班)的4位同學對該校部分學生進行了隨機調查,按“騎自行車”、“乘公交車”、“步行”、“乘私家車”、“其他方式”設置選項.要求被調查的所有學生從中選一項,并將調查結果繪制成了條形統計圖1和扇形統計圖2.根據所提供的信息,解答下列問題.
(1)本次調查的人數共有___________人,扇形中步行的圓心角度度數為________.
(2)把條形統計圖補充完整.
(3)若該校共有學生3000人,則全校步行的學生大約有多少人數?
(4)根據調查結果對學生的環保出行提一條合理化的建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,完成任務:
自相似圖形
定義:若某個圖形可分割為若干個都與它相似的圖形,則稱這個圖形是自相似圖形.例如:正方形ABCD中,點E、F、G、H分別是AB、BC、CD、DA邊的中點,連接EG,HF交于點O,易知分割成的四個四邊形AEOH、EBFO、OFCG、HOGD均為正方形,且與原正方形相似,故正方形是自相似圖形.
任務:
(1)圖1中正方形ABCD分割成的四個小正方形中,每個正方形與原正方形的相似比為 ;
(2)如圖2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明發現△ABC也是“自相似圖形”,他的思路是:過點C作CD⊥AB于點D,則CD將△ABC分割成2個與它自己相似的小直角三角形.已知△ACD∽△ABC,則△ACD與△ABC的相似比為 ;
(3)現有一個矩形ABCD是自相似圖形,其中長AD=a,寬AB=b(a>b).
請從下列A、B兩題中任選一條作答:我選擇 題.
A:①如圖3﹣1,若將矩形ABCD縱向分割成兩個全等矩形,且與原矩形都相似,則a= (用含b的式子表示);
②如圖3﹣2若將矩形ABCD縱向分割成n個全等矩形,且與原矩形都相似,則a= (用含n,b的式子表示);
B:①如圖4﹣1,若將矩形ABCD先縱向分割出2個全等矩形,再將剩余的部分橫向分割成3個全等矩形,且分割得到的矩形與原矩形都相似,則a= (用含b的式子表示);
②如圖4﹣2,若將矩形ABCD先縱向分割出m個全等矩形,再將剩余的部分橫向分割成n個全等矩形,且分割得到的矩形與原矩形都相似,則a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
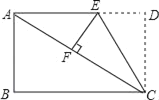
【題目】如圖,在矩形ABCD中,AB=6,BC=8,將矩形ABCD沿CE折疊后,使點D恰好落在對角線AC上的點F處.
(1)求EF的長;
(2)求梯形ABCE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com