【題目】已知：
，
是關于
的方程
的兩個不相等的實數根，當
取最小整數時，則
的值為________．
【答案】-2015
【解析】
根據一元二次方程的定義和判別式的意義得到m-1≠0且△=22-4（m-1）（-1）>0，解不等式求出m>0且m≠1，那么m滿足條件的最小整數為2，則原方程化為x2+2x-1=0，再根據一元二次方程的解的定義以及根與系數的關系得出a2+2a-1=0，a+b=-2，即a2+2a=1，然后將a3-a2+7b-1998變形為a（a2+2a）-3a2+7b-1998=a-3a2+7b-1998=-3（a2+2a）+7（a+b）-1998，代入計算即可．
根據題意得m1≠0且△=224(m1)(1)>0，
解得m>0且m≠1；
所以m滿足條件的最小整數為2,則原方程化為x2+2x1=0，
∵a，b是方程的兩個根，
∴a2+2a1=0，a+b=2，
∴a2+2a=1，
a3a2+7b1998
=a(a2+2a)3a2+7b1998
=a3a2+7b1998
=3(a2+2a)+7a+7b1998
=3+7(a+b)1998
=3+7×(2)1998
=2015.
故答案為:2015.
科目：初中數學 來源： 題型：
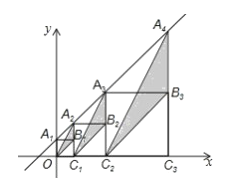
【題目】在直角坐標系中，直線
與y軸交于點
，按如圖方式作正方形
、
、
、…，點、
、
、…在直線上，點
、
、
、…，在x軸上，圖中陰影部分三角形的面積從左到右依次記為
、
、
、…
，則
_______，
________.（用含n的代數式表示，n為正整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
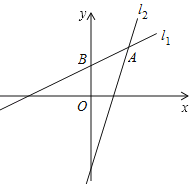
【題目】已知直線l1：y1＝
x+3經過點A（m，5），與y軸的交點為B；直線l2：y2＝kx+b經過點A和C（2，﹣1）．
（1）求直線l2的解析式，并直接寫出不等式y1≥y2的解集；
（2）求△AOB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
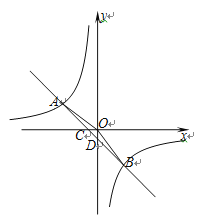
【題目】如圖，在平面直角坐標系中，一次函數
的圖象與反比例函數
的圖象交于第二、四象限內的A，B兩點，與x軸交于點C，與y軸交于點D，點B的坐標是（m，﹣4），連接AO，AO=5，sin∠AOC=
．
（1）求反比例函數的解析式
（2）連接OB，求△AOB的面積
(3) 根據圖象直接寫出當
時，x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
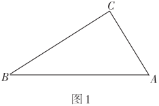
【題目】圖形的折疊即圖形的翻折或者說是對稱變換.這類問題與生活緊密聯系，內容豐富，解法靈活，具有開放性，可以培養我們的動手能力，空間想象能力和幾何變換的思想.在綜合與實踐課上，每個小組剪了一些如圖1所示的直角三角形紙片（
，
，
），并將
紙片中的各內角進行折疊操作：
（1）如圖2，“奮斗”小組將紙片中的
進行折疊，使直角邊
落在斜邊
上，點
落在點
位置，折痕為
，則
的長為______
.
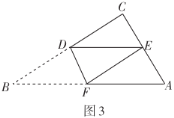
（2）如圖3，“勤奮”小組將中的
進行折疊，使點
落在直角邊中點上，折痕為
，則
的長為______.
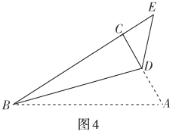
（3）如圖4，“雄鷹”小組將紙片中的
進行折疊，使點
落在直角邊
延長線上的點處，折痕為，求出的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示是二次函數
圖象的一部分，圖象過
點
，二次函數圖象對稱軸為直線
，給出五個結論：①
；②
；③
；④方程
的根為
，
；⑤當
時，
隨著
的增大而增大．其中正確結論是（ ）
A. ①②③ B. ①③④ C. ②③④ D. ①④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
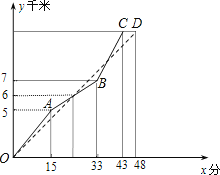
【題目】如圖表示甲、乙兩名選手在一次自行車越野賽中，路程y（千米）隨時間x（分）變化的圖象．下面幾個結論：①比賽開始24分鐘時，兩人第一次相遇．②這次比賽全程是10千米．③比賽開始38分鐘時，兩人第二次相遇．正確的結論為_____（只填序號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在四邊形ABCD中，AB＝BC，AD2+CD2＝2AB2，CD⊥AD．
（1）求證：AB⊥BC．
（2）若AB＝3CD，AD＝17，求四邊形ABCD的周長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
