
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上一點(diǎn),且
邊上一點(diǎn),且![]() .點(diǎn)
.點(diǎn)![]() 是直線
是直線![]() 上一點(diǎn)且在點(diǎn)
上一點(diǎn)且在點(diǎn)![]() 的右側(cè),
的右側(cè),![]() ,點(diǎn)
,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿射線
出發(fā),沿射線![]() 方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為
方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒.以
秒.以![]() 為圓心,
為圓心,![]() 為半徑作半圓
為半徑作半圓![]() ,交直線
,交直線![]() 分別于點(diǎn)
分別于點(diǎn)![]() ,
,![]() (點(diǎn)
(點(diǎn)![]() 在
在![]() 的左側(cè)).
的左側(cè)).
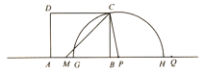
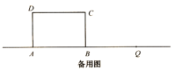
(1)當(dāng)![]() 秒時(shí),
秒時(shí),![]()
![]() 的長(zhǎng)等于__________,
的長(zhǎng)等于__________,![]() __________秒時(shí),半圓
__________秒時(shí),半圓![]() 與
與![]() 相切;
相切;
(2)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),求半圓
重合時(shí),求半圓![]() 被矩形
被矩形![]() 的對(duì)角線
的對(duì)角線![]() 所截得的弦長(zhǎng);
所截得的弦長(zhǎng);
(3)若![]() ,求扇形
,求扇形![]() 的面積.
的面積.
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() ,
,![]() ;(2)當(dāng)點(diǎn)
;(2)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),半圓
重合時(shí),半圓![]() 被矩形
被矩形![]() 的對(duì)角線
的對(duì)角線![]() 所截得的弦長(zhǎng)為
所截得的弦長(zhǎng)為![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)先根據(jù)線段的和差求出BP的長(zhǎng),再根據(jù)勾股定理即可求出PC的長(zhǎng);先根據(jù)圓的性質(zhì)、勾股定理求出BP的長(zhǎng),再根據(jù)線段的和差求出PQ的長(zhǎng),由此即可求出t的值;
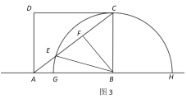
(2)如圖3(見解析),先在![]() 中,求出
中,求出![]() ,從而可得
,從而可得![]() ,再根據(jù)直角三角形的性質(zhì)求出
,再根據(jù)直角三角形的性質(zhì)求出![]() ,然后根據(jù)正弦三角函數(shù)值求出CF的長(zhǎng),最后根據(jù)垂徑定理即可得;
,然后根據(jù)正弦三角函數(shù)值求出CF的長(zhǎng),最后根據(jù)垂徑定理即可得;
(3)先依題意分兩種情況,再分別根據(jù)三角形的外角性質(zhì)求出![]() 的度數(shù),然后根據(jù)直角三角形的性質(zhì)求出PC的長(zhǎng),最后根據(jù)扇形的面積公式求解即可得.
的度數(shù),然后根據(jù)直角三角形的性質(zhì)求出PC的長(zhǎng),最后根據(jù)扇形的面積公式求解即可得.
(1)![]() 四邊形ABCD是矩形
四邊形ABCD是矩形
![]()
![]()
當(dāng)![]() 秒時(shí),
秒時(shí),![]()
![]()
![]()
若半圓![]() 與
與![]() 相切,則點(diǎn)P在線段AB上,且
相切,則點(diǎn)P在線段AB上,且![]()
設(shè)![]() ,則
,則![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
故答案為:![]() ,
,![]() ;
;
(2)如圖3,過點(diǎn)![]() 作
作![]() 于
于![]()
在![]() 中,
中,![]()
![]() ,
,![]()
![]() 在
在![]() 中,
中,![]()
![]() ,即
,即![]()
![]()
由垂徑定理可得:![]()
故當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),半圓
重合時(shí),半圓![]() 被矩形
被矩形![]() 的對(duì)角線
的對(duì)角線![]() 所截得的弦長(zhǎng)為
所截得的弦長(zhǎng)為![]() ;
;
(3)若![]() ,分以下兩種情況:
,分以下兩種情況:
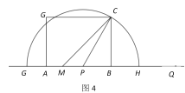
①如圖4,![]()
![]()
在![]() 中,
中,![]()
則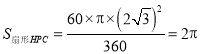
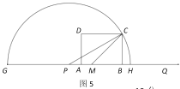
②如圖5,![]()
![]()
在![]() 中,
中,![]()
則![]()
綜上,扇形![]() 的面積為
的面積為![]() 或
或![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】從長(zhǎng)度為3、5、7、8的四條線段中任意選三條組成三角形,其中能組成含有60°角的三角形的概率為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,圖1中小黑點(diǎn)的個(gè)數(shù)記為![]() ,圖2中小黑點(diǎn)的個(gè)數(shù)記為
,圖2中小黑點(diǎn)的個(gè)數(shù)記為![]() ,圖3中小黑點(diǎn)的個(gè)數(shù)記為
,圖3中小黑點(diǎn)的個(gè)數(shù)記為![]() ,…
,…
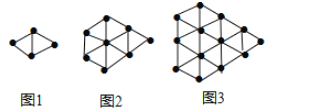
根據(jù)以上圖中的規(guī)律完成下列問題:
(1)圖4中小黑點(diǎn)的個(gè)數(shù)記為![]() ,則
,則![]() __________;
__________;
(2)圖![]() 中小黑點(diǎn)的個(gè)數(shù)記為
中小黑點(diǎn)的個(gè)數(shù)記為![]() ,則
,則![]() ___________(用含
___________(用含![]() 的式子表示);
的式子表示);
(3)若第![]() 個(gè)圖形中小黑點(diǎn)的個(gè)數(shù)比它前一個(gè)圖形中小黑點(diǎn)的個(gè)數(shù)多100,則
個(gè)圖形中小黑點(diǎn)的個(gè)數(shù)比它前一個(gè)圖形中小黑點(diǎn)的個(gè)數(shù)多100,則![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
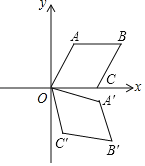
【題目】如圖,在平面直角坐標(biāo)系xOy中,菱形OABC的邊長(zhǎng)為2,點(diǎn)A在第一象限,點(diǎn)C在x軸正半軸上,∠AOC=60°,若將菱形OABC繞點(diǎn)O順時(shí)針旋轉(zhuǎn)75°,得到四邊形OA′B′C′,則點(diǎn)B的對(duì)應(yīng)點(diǎn)B′的坐標(biāo)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
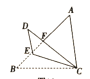
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .則
.則![]() 的長(zhǎng)為__________;若
的長(zhǎng)為__________;若![]() 是
是![]() 邊上一點(diǎn),將
邊上一點(diǎn),將![]() 沿
沿![]() 所在直線翻折得到
所在直線翻折得到![]() ,
,![]() 交
交![]() 于
于![]() ,則當(dāng)
,則當(dāng)![]() 時(shí),
時(shí),![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
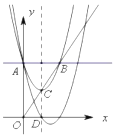
【題目】如圖,拋物線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,與過點(diǎn)
,與過點(diǎn)![]() 平行于
平行于![]() 軸的直線相交于點(diǎn)
軸的直線相交于點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 在第一象限).拋物線的頂點(diǎn)
在第一象限).拋物線的頂點(diǎn)![]() 在直線
在直線![]() 上,對(duì)稱軸與
上,對(duì)稱軸與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() .平移拋物線,使其經(jīng)過點(diǎn)
.平移拋物線,使其經(jīng)過點(diǎn)![]() 、
、![]() ,則平移后的拋物線的解析式為__________.
,則平移后的拋物線的解析式為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
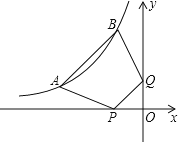
【題目】如圖,點(diǎn)A(a,1),B(b,3)都在雙曲線y=﹣![]() 上,點(diǎn)P,Q分別是x軸,y軸上的動(dòng)點(diǎn),則四邊形ABPQ周長(zhǎng)的最小值為( )
上,點(diǎn)P,Q分別是x軸,y軸上的動(dòng)點(diǎn),則四邊形ABPQ周長(zhǎng)的最小值為( )
A.4![]() B.6
B.6![]() C.2
C.2![]() +2
+2![]() D.8
D.8![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)因式分解:![]() ___________.
___________.
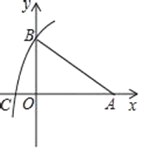
(2)如圖,在平面直角坐標(biāo)系中,A(6,0),B(0,2![]() ),以點(diǎn)A為圓心,AB長(zhǎng)為半徑畫弧,交x軸的負(fù)半軸于點(diǎn)C,則點(diǎn)C坐標(biāo)為_______.扇形BAC的面積為______.
),以點(diǎn)A為圓心,AB長(zhǎng)為半徑畫弧,交x軸的負(fù)半軸于點(diǎn)C,則點(diǎn)C坐標(biāo)為_______.扇形BAC的面積為______.
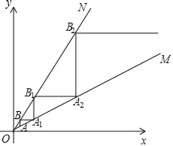
(3)在平面直角坐標(biāo)系中,點(diǎn)![]() 在射線OM上,點(diǎn)
在射線OM上,點(diǎn)![]() 在射線ON上,以AB為直角邊作Rt△ABA1,以BA1為直角邊作第二個(gè)Rt△BA1B1,則點(diǎn)B1的縱坐標(biāo)為________,然后以A1B1為直角邊作第三個(gè)Rt△A1B1A2,…,依次規(guī)律,得到Rt△B2019A2020B2020,則點(diǎn)B2020的縱坐標(biāo)為_______.
在射線ON上,以AB為直角邊作Rt△ABA1,以BA1為直角邊作第二個(gè)Rt△BA1B1,則點(diǎn)B1的縱坐標(biāo)為________,然后以A1B1為直角邊作第三個(gè)Rt△A1B1A2,…,依次規(guī)律,得到Rt△B2019A2020B2020,則點(diǎn)B2020的縱坐標(biāo)為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC 中,AB=AC,點(diǎn) M 在 BA 的延長(zhǎng)線上,點(diǎn) N 在 BC 的延長(zhǎng)線上,過點(diǎn) C 作CD∥AB 交∠CAM 的平分線于點(diǎn) D.
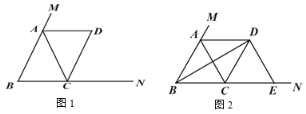
(1)如圖 1,求證:四邊形 ABCD 是平行四邊形;
(2)如圖 2,當(dāng)∠ABC=60°時(shí),連接 BD,過點(diǎn) D 作 DE⊥BD,交 BN 于點(diǎn) E,在不添加任何輔助線的情況下,請(qǐng)直接寫出圖 2 中四個(gè)三角形(不包含△CDE),使寫出的每個(gè)三角形的面積與△CDE 的面積相等.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com