
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() ,
,![]() ,
,![]() ,
,![]() 分別在正方形的四條邊上,且
分別在正方形的四條邊上,且![]() ,則四邊形
,則四邊形![]() 的形狀為________,它的面積的最小值為________.
的形狀為________,它的面積的最小值為________.

【答案】正方形![]()
【解析】
先證明△AEH≌△DFE≌△CGF≌△BHG,從而得到HE=EF=FG=HG,然后證明EFGH四邊形有一個角是直角,從而可判斷出四邊形EFGH的形狀,設AE=x,則AH=(![]() -x),依據正方形的面積公式以及勾股定理可得到四邊形EFGH的面積與x的函數關系式,依據二次函數的性質求得二次函數的最小值即可.
-x),依據正方形的面積公式以及勾股定理可得到四邊形EFGH的面積與x的函數關系式,依據二次函數的性質求得二次函數的最小值即可.
∵四邊形ABCD是正方形,
∴AB=BC=CD=AD, ∠A=∠B=∠C=∠D.
∵AE=DF=CG=BH,
∴AH=ED=FG=BG.
在△AEH、△DFE、△CGF、△BHG中,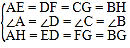 ,
,
∴△AEH≌△DFE≌CGF≌△BHG.
∴HE=EF=FG=HG.
∴四邊形EFGH是菱形.
∵△AEH≌△DFE,
∴∠AEH=∠DFE.
∵∠AHE+∠AEH=90°,
∴∠DEF+∠AEH=90°.
∴∠HEF=90°.
∴EHGF為正方形.
設AE=x,則AH=(![]() -x).
-x).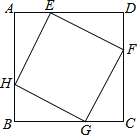
∵正方形EFHG的面積=HE=AE+AH=x+(![]() -x) =2x-2
-x) =2x-2![]() x+5,
x+5,
∴當x=![]() 時,正方形的面積有最小值.
時,正方形的面積有最小值.
∴正方形EFHG的面積的最小值=![]() .
.
故答案為:正方形;![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】有一個安裝有進出水管的30升容器,水管每單位時間內進出的水量是一定的,設從某時刻開始的4分鐘內只進水不出水,在隨后的8分鐘內既進水又出水,得到水量y(升)與時間x(分)之間的函數關系如圖所示根據圖象信息給出下列說法:
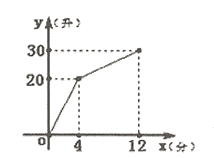
①每分鐘進水5升;
②當![]() 時,容器中水量在減少;
時,容器中水量在減少;
③若12分鐘后只放水,不進水,還要8分鐘可以把水放完;
④若從一開始進出水管同時打開需要24分鐘可以將容器灌滿.
以下說法中正確的有( )
A.①B.①②C.①④D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(定義)配方法是指將一個式子或一個式子的某一部分通過恒等變形化為完全平方式或幾個完全平
方式的和,這種方法稱之為配方法,例如:可將多項式![]() 通過橫檔變形化為
通過橫檔變形化為![]() 的形式,這個變形過程中應用了配方法.
的形式,這個變形過程中應用了配方法.
(1)(理解)對于多項式![]() ,當x=____________時,它的最小值為______________.
,當x=____________時,它的最小值為______________.
(2)(應用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三邊,且有
的三邊,且有![]() .
.
①若c為整數,求c的值.
②直接寫出這個三角形的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2012年“國際攀巖比賽”在重慶舉行.小麗從家出發開車前去觀看,途中發現忘了帶門票,于是打電話讓媽媽馬上從家里送來,同時小麗也往回開,遇到媽媽后聊了一會兒,接著繼續開車前往比賽現場.設小麗從家出發后所用時間為t,小麗與比賽現場的距離為S.下面能反映S與t的函數關系的大致圖象是( )
A. B.
B.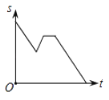 C.
C. D.
D.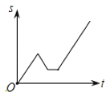
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩同學從A地出發,騎自行車在同一條路上行駛到B地,他們離出發地的距離s(千米)和行駛時間t(小時)之間的函數關系圖象如圖所示,根據圖中提供的信息,有下列說法:

(1)他們都行駛了18千米;
(2)甲在途中停留了0.5小時;
(3)乙比甲晚出發了0.5小時;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙兩人同時到達目的地
其中符合圖象描述的說法有( )
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
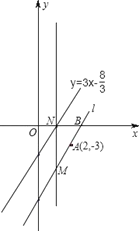
【題目】如圖,在平面直角坐標系中,直線 l 經過點A(2,﹣3),與 x 軸交于點 B,且與直線y=3x-![]() 平行.
平行.
(1)求直線l的函數解析式及點B的坐標;
(2)如直線l上有一點 M(a,﹣6),過點 M 作 x 軸的垂線,交直線 y=3x-![]() 于點N,在線段MN上求一點P,使△PAB是直角三角形,請求出點P的坐標.
于點N,在線段MN上求一點P,使△PAB是直角三角形,請求出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com