
【題目】閱讀材料,回答問題
在邊長為1的正方形ABCD中,E是AB的中點,CF⊥DE,F為垂足.
(1)△CDF與△DEA是否相似?說明理由;
(2)求CF的長.
【答案】
(1)解:△ADE∽△FCD,理由如下:
∵四邊形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD
(2)解:由題意知,AD=CD=1,AE= ![]() .
.
在直角△DEA中,有DE= ![]() =
= ![]() =
= ![]() .
.
由(1)可得: ![]() =
= ![]() ,則CF=
,則CF= ![]() =
= ![]()
【解析】(1)利用正方形的性質和平行線的性質,由兩角法證明△ADE∽△FCD;
(2)根據勾股定理及相似三角形對應邊成比例求解。
【考點精析】關于本題考查的勾股定理的概念和正方形的性質,需要了解直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形才能得出正確答案.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
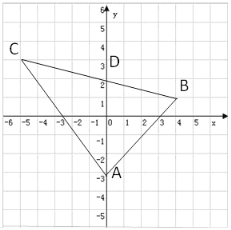
【題目】如圖所示的平面直角坐標系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面積;
(2) 點M是平面直角坐標系第一象限內的一動點,點M的縱坐標為3,三角形BCM的面積為6,求點M的坐標;
(3) 記BC與y軸的交點為D,求點D的坐標(寫出具體解答過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,在△ABC中,∠C=60°,∠A=40°.

(1)用尺規作圖作AB的垂直平分線,交AC于點D,交AB于點E(保留作圖痕跡,不要求寫作法和證明);
(2)求證:BD平分∠CBA.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學的許多創新和發展都位居世界前列,如南宋數學家楊輝揭示了二項和![]() 的展開式的各項系數規律,比歐洲的發現早三百年,為紀念楊輝的功績,世人稱如圖中右圖叫“楊輝三角”。
的展開式的各項系數規律,比歐洲的發現早三百年,為紀念楊輝的功績,世人稱如圖中右圖叫“楊輝三角”。
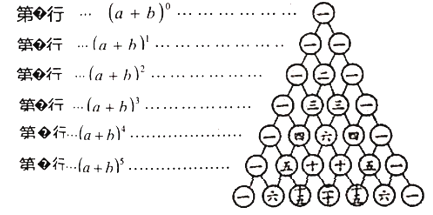
(1)觀察“楊輝三角”規律,依次寫出“楊輝三角”第![]() 行中從左到右的各數;
行中從左到右的各數;
(2)請運用冪的意義和多項式乘法法則,按如下要求展開下列各式,以驗證“楊輝三角”第四行的規律:展開后各項按字母![]() 降冪、
降冪、![]() 升冪排列
升冪排列![]()
(3)解不等式![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某小區某月家庭用水量的情況,從該小區隨機抽取部分家庭進行調查,以下是根據調查數據繪制的統計圖表的一部分
分組 | 家庭用水量x/噸 | 家庭數/戶 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根據以上信息,解答下列問題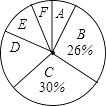
(1)家庭用水量在4.0<x≤6.5范圍內的家庭有戶,在6.5<x≤9.0范圍內的家庭數占被調查家庭數的百分比是 %;
(2)本次調查的家庭數為戶,家庭用水量在9.0<x≤11.5范圍內的家庭數占被調查家庭數的百分比是 %;
(3)家庭用水量的中位數落在組;
(4)若該小區共有200戶家庭,請估計該月用水量不超過9.0噸的家庭數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的箱子里共有3個球,其中2個白球,1個紅球,它們除顏色外均相同.
(1)從箱子中隨機摸出一個球是白球的概率是多少?
(2)從箱子中隨機摸出一個球,記錄下顏色后不將它放回箱子,攪勻后再摸出一個球,求兩次摸出的球都是白球的概率,并畫出樹狀圖.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com