
【題目】如圖示,三角形ABC是等邊三角形,D是BC邊上的一點,三角形ABD經過旋轉后到達三角形ACE的位置.
(1)旋轉中心是哪一點?
(2)旋轉了多少度?
(3)如果M是AB的中點,那么經過上述旋轉后,點M到了什么位置?

【答案】(1)點A;(2)60°;(3)點M到了AC的中點處.
【解析】(1)觀察圖形,由于△ABC是等邊三角形,D是BC上一點,△ABD經旋轉后到達△ACE的位置,可得出旋轉中心;
(2)觀察圖形,線段AB旋轉后,對應邊是AC,∠BAC就是旋轉角,可得出旋轉角;
(3)因為旋轉前后AB、AC是對應邊,故AB的中點M,旋轉后就是AC的中點了.
(1)∵△ABD經旋轉后到達△ACE,它們的公共頂點為A,
∴旋轉中心是點A;
(2)線段AB旋轉后,對應邊是AC,∠BAC就是旋轉角,也是等邊三角形的內角,是60°,
∴旋轉了60°;
(3)∵旋轉前后AB,AC是對應邊,故AB的中點M,旋轉后就是AC的中點了,
∴點M轉到了AC的中點.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案科目:初中數學 來源: 題型:
【題目】(1)觀察思考
如圖所示,線段AB上的點數與線段的總條數有如下關系:如果線段AB上有3個點,那么線段總條數為3;如果線段AB上有4個點,那么線段總條數為6;如果線段AB上有5個點,那么線段總條數為________.
![]() 3=2+1=
3=2+1=![]()
![]() 6=3+2+1=
6=3+2+1=![]()
![]()
(2)模型構建
如果線段上有m個點(包括線段的兩個端點),那么共有________條線段.
(3)拓展應用
8位同學參加班上組織的象棋比賽,比賽采用單循環制(即每兩位同學之間都要進行一場比賽),那么一共要進行多少場比賽?
請將這個問題轉化為上述模型,并直接應用上述模型的結論解決問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,BE⊥AC于點E,AD⊥BC于點D,
∠BAD=45°,AD與BE交于點F,連接CF.
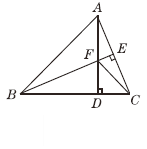
(1)求證:BF=2AE;
(2)若CD=![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分類
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整數:{ …}
(2)負整數:{ …}
(3)整數:{ …}
(4)分數:{ …}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線C1:y=a(x+1)(x﹣3a)(a>0)與x軸交于A,B兩點(A在B的左側),與y軸交于點C(0,﹣3)
(1)求拋物線C1的解析式及A,B點坐標;
(2)求拋物線C1的頂點坐標;
(3)將拋物線C1向上平移3個單位長度,再向左平移n(n>0)個單位長度,得到拋物線C2 , 若拋物線C2的頂點在△ABC內,求n的取值范圍. (在所給坐標系中畫出草圖C1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形ABCD中,動點F,E分別以相同的速度從D,C兩點同時出發向C和B運動(任何一個點到達即停止),過點P作PM∥CD交BC于M點,PN∥BC交CD于N點,連接MN,在運動過程中, ①AE和BF的位置關系為;
②線段MN的最小值為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果∠A和∠B互補,且∠A>∠B,給出下列四個式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.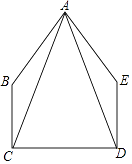
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com