
【題目】正方形ABCD中,點(diǎn)O是對(duì)角線AC的中點(diǎn),P是對(duì)角線AC上一動(dòng)點(diǎn),過(guò)點(diǎn)P作PF⊥CD于點(diǎn)F.如圖1,當(dāng)點(diǎn)P與點(diǎn)O重合時(shí),顯然有DF=CF.
(1)如圖2,若點(diǎn)P在線段AO上(不與點(diǎn)A、O重合),PE⊥PB且PE交CD于點(diǎn)E.
①求證:DF=EF;
②寫出線段PC、PA、CE之間的一個(gè)等量關(guān)系;并說(shuō)出理由;
(2)若點(diǎn)P在線段OC上(不與點(diǎn)O、C重合),PE⊥PB且PE交直線CD于點(diǎn)E.請(qǐng)完成圖3并判斷(1)中的結(jié)論①、②是否分別成立?若不成立,寫出相應(yīng)的結(jié)論.(所寫結(jié)論均不必證明)

【答案】(1)①證明見解析;②PC=![]() CE+PA;(2)結(jié)論成立.
CE+PA;(2)結(jié)論成立.
【解析】整體分析:
(1)連接PD,通過(guò)△BCP≌△DCP證得∠PBC=∠PDC,由四邊形PBCE的內(nèi)角得到∠PED=∠PBC,即可證PD=PE,由等腰三角形的“三線合一”即可;(2)延長(zhǎng)FP交AB于點(diǎn)G,由PC與CF的關(guān)系,結(jié)合EF=DF=AG逐漸轉(zhuǎn)化得到這三條線段間的數(shù)量關(guān)系;(3)根據(jù)題意畫出圖形,對(duì)比(2)中的結(jié)論求解.
解:(1)①連接PD,
∵四邊形ABCD是正方形,AC平分∠BCD,CB=CD,△BCP≌△DCP,
∴∠PBC=∠PDC,PB=PD
∵PB⊥PE,∠BCD=90°,
∴∠PBC+∠PEC=360°-∠BPE-∠BCE=180°,
∴∠PED=∠PBC=∠PDC,∴PD=PE,
∵PF⊥CD,∴DF=EF

②PC=![]() CE+PA,理由如下:
CE+PA,理由如下:
延長(zhǎng)FP交AB于點(diǎn)G,則四邊形ADFG是矩形,∴AG=DF.
∵△AGP是等腰直角三角形,∴AG=![]() AP.
AP.
∵△FCP是等腰直角三角形,
∴CP=![]() CF=
CF=![]() (CE+EF)
(CE+EF)
=![]() (CE+DF)=
(CE+DF)= ![]() (CE+AG)
(CE+AG)
=![]() (CE+
(CE+![]() AP)
AP)
=![]() CE+PA.
CE+PA.

(3)結(jié)論①成立,結(jié)論②不成立,此時(shí)②中的三條線段之間的數(shù)量關(guān)系為PA=![]() CE+PC.
CE+PC.




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】解不等式組.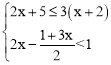 把不等式組的解集在數(shù)軸上表示出來(lái),并寫出不等式組的非負(fù)整數(shù)解.
把不等式組的解集在數(shù)軸上表示出來(lái),并寫出不等式組的非負(fù)整數(shù)解.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,下面的圖象記錄了某地一月份某大的溫度隨時(shí)間變化的情況,請(qǐng)你仔細(xì)觀察圖象回答下面的問(wèn)題:

(1)在這個(gè)問(wèn)題中,變量分別是______,時(shí)間的取值范圍是______;
(2)20時(shí)的溫度是______℃,溫度是0℃的時(shí)刻是______時(shí),最暖和的時(shí)刻是_______時(shí),溫度在-3℃以下的持續(xù)時(shí)間為______小時(shí);
(3)你從圖象中還能獲得哪些信息?(寫出1~2條即可)
答:__________________________________________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在邊長(zhǎng)為1個(gè)單位長(zhǎng)度的小正方形組成的網(wǎng)格中,點(diǎn)A、B、C都是格點(diǎn).
(1)將△ABC向左平移6個(gè)單位長(zhǎng)度得到△A 1B 1C 1,請(qǐng)?jiān)诰W(wǎng)格中畫出△A 1B 1C 1
(2)將△ABC繞點(diǎn)O按逆時(shí)針?lè)较蛐D(zhuǎn)180°得到△A 2B 2C 2,請(qǐng)?jiān)诰W(wǎng)格畫出△A 2B 2C 2.
(3)請(qǐng)問(wèn)△A 1B 1C 1與△A 2B 2C 2成中心對(duì)稱嗎?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
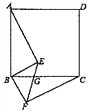
【題目】如圖,四邊形ABCD是正方形,BE⊥BF,BE=BF,EF與BC交于點(diǎn)G.
(1)求證:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于反比例函數(shù)![]() ,下列說(shuō)法不正確的是( )
,下列說(shuō)法不正確的是( )
A. 點(diǎn)(-2,-1)在它的圖像上 B. 它的圖像在第一、三象限
C. 當(dāng)![]() 時(shí),y隨x的增大而增大 D. 當(dāng)
時(shí),y隨x的增大而增大 D. 當(dāng)![]() 時(shí),y隨x的增大而減小
時(shí),y隨x的增大而減小
【答案】C
【解析】試題分析:反比例函數(shù)![]() 的性質(zhì):當(dāng)
的性質(zhì):當(dāng)![]() 時(shí),圖象在一、三象限,在每一象限,y隨x的增大而減小;當(dāng)
時(shí),圖象在一、三象限,在每一象限,y隨x的增大而減小;當(dāng)![]() 時(shí),圖象在二、四象限,在每一象限,y隨x的增大而增大.
時(shí),圖象在二、四象限,在每一象限,y隨x的增大而增大.
A.點(diǎn)![]() 在它的圖象上,B.它的圖象在第一、三象限,C.當(dāng)
在它的圖象上,B.它的圖象在第一、三象限,C.當(dāng)![]() 時(shí),
時(shí),![]() 隨
隨![]() 的增大而減小,均正確,不符合題意;
的增大而減小,均正確,不符合題意;
D.當(dāng)![]() 時(shí),
時(shí),![]() 隨
隨![]() 的增大而減小,故錯(cuò)誤,本選項(xiàng)符合題意.
的增大而減小,故錯(cuò)誤,本選項(xiàng)符合題意.
考點(diǎn):反比例函數(shù)的性質(zhì)
點(diǎn)評(píng):本題屬于基礎(chǔ)應(yīng)用題,只需學(xué)生熟練掌握反比例函數(shù)的性質(zhì),即可完成.
【題型】單選題
【結(jié)束】
8
【題目】如圖,雙曲線![]() (x<0)經(jīng)過(guò)平行四邊形ABCO的對(duì)角線交點(diǎn)D,已知邊OC在y軸上,且AC⊥AB于點(diǎn)C,則平行四邊形ABCO的面積是( )
(x<0)經(jīng)過(guò)平行四邊形ABCO的對(duì)角線交點(diǎn)D,已知邊OC在y軸上,且AC⊥AB于點(diǎn)C,則平行四邊形ABCO的面積是( )

A. ![]() B.
B. ![]() C. 3 D. 6
C. 3 D. 6
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】當(dāng)m=________時(shí),函數(shù)![]() 是反比例函數(shù).
是反比例函數(shù).
【答案】2
【解析】試題分析:∵函數(shù)y=(m+2)x|m|-3是反比例函數(shù),
∴m+2≠0且|m|-3=-1,
解得m=2.
故答案為2.
點(diǎn)睛:本題考查了反比例函數(shù)的定義:若兩個(gè)變量x與y滿足y=![]() (k≠0)的關(guān)系式,則y與x稱為反比例函數(shù).
(k≠0)的關(guān)系式,則y與x稱為反比例函數(shù).
【題型】填空題
【結(jié)束】
12
【題目】為弘揚(yáng)中華傳統(tǒng)文化,某校組織八年級(jí)1000名學(xué)生參加漢字聽寫大賽.為了解學(xué)生整體聽寫能力,從中抽取部分學(xué)生的成績(jī)(得分取正整數(shù),滿分為100分)進(jìn)行統(tǒng)計(jì)分析,得到分?jǐn)?shù)段在70.5~80.5的頻數(shù)是50,所占百分比25%,則本次抽樣調(diào)查的樣本容量為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】關(guān)于x的分式方程![]() =1的解是正數(shù),則m的取值范圍是_____.
=1的解是正數(shù),則m的取值范圍是_____.
【答案】m<1
【解析】試題分析:去分母得:2x+m=x-2,
解得:x=-m-2,
∵關(guān)于x的方程![]() =1的解是正數(shù),
=1的解是正數(shù),
∴-m-2>0,
解得m<-2,
又∵x=-m-2≠2,
∴m≠-4,
∴m的取值范圍是:m<-2且m≠-4.
故答案為:m<-2且m≠-4.
點(diǎn)睛:此題主要考查了分式方程的解,要熟練掌握,解答此題的關(guān)鍵是要明確:在解方程的過(guò)程中因?yàn)樵诎逊质椒匠袒癁檎椒匠痰倪^(guò)程中,擴(kuò)大了未知數(shù)的取值范圍,可能產(chǎn)生增根,增根是令分母等于0的值,不是原分式方程的解.
【題型】填空題
【結(jié)束】
18
【題目】若關(guān)于x的分式方程 ![]() 無(wú)解,則m的值為_______.
無(wú)解,則m的值為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】利用如圖1的二維碼可以進(jìn)行身份識(shí)別.某校建立了一個(gè)身份識(shí)別系統(tǒng),圖2是某個(gè)學(xué)生的識(shí)別圖案,黑色小正方形表示1,白色小正方形表示0.將第一行數(shù)字從左到右依次記為![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以轉(zhuǎn)換為該生所在班級(jí)序號(hào),其序號(hào)為
,那么可以轉(zhuǎn)換為該生所在班級(jí)序號(hào),其序號(hào)為![]() .如圖2第一行數(shù)字從左到右依次為0,1,0,1,序號(hào)為
.如圖2第一行數(shù)字從左到右依次為0,1,0,1,序號(hào)為![]() ,表示該生為5班學(xué)生.表示6班學(xué)生的識(shí)別圖案是( )
,表示該生為5班學(xué)生.表示6班學(xué)生的識(shí)別圖案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com