
【題目】若方程(m+2)xm+3mx+1=0是關于x的一元二次方程,則( )
A.m=±2 B.m=﹣2 C.m=2 D.m≠±2
科目:初中數學 來源: 題型:
【題目】探索與研究:
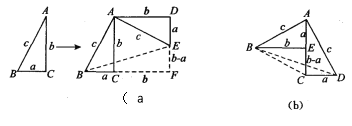
方法1:如圖(a),對任意的符合條件的直角三角形繞其銳角頂點旋轉90°所得,所以
∠BAE=90°,且四邊形ACFD是一個正方形,它的面積和四邊形ABFE面積相等,而四邊形ABFE面積等于Rt△BAE和Rt△BFE的面積之和,根據圖示寫出證明勾股定理的過程;
方法2:如圖(b),是任意的符合條件的兩個全等的Rt△BEA和Rt△ACD拼成的,你能根據圖示再寫一種證明勾股定理的方法嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標分別為A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
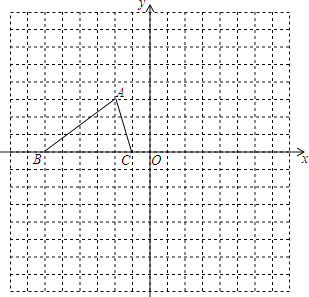
(1)將△ABC沿y軸翻折,則翻折后點A的對應點的坐標是 .
(2)作出△ABC關于x軸對稱的圖形△A1B1C1,畫△A1B1C1,并直接寫出點A1的坐標.
(3)若以D、B、C為頂點的三角形與△ABC全等,請畫出所有符合條件的△DBC(點D與點A重合除外),并直接寫出點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知m,n是方程x2﹣2x﹣1=0的兩根,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,則a的值等于( )
A.﹣5 B.5 C.﹣9 D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列判斷不正確的是( )
A. 形狀相同的圖形是全等圖形 B. 能夠完全重合的兩個三角形全等
C. 全等圖形的形狀和大小都相同 D. 全等三角形的對應角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,BD是△ABC的一條角平分線.點O、E、F分別在BD、BC、AC上,且四邊形OECF是正方形.
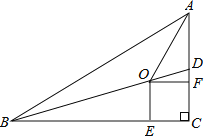
(1)求證:點O在∠BAC的平分線上;
(2)若AC=5,BC=12,求OE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com