
【題目】(1)請用兩種不同的方法列代數(shù)式表示圖中陰影部分的面積.

方法①_________________;
方法②_________________;
(2)根據(jù)(1)寫出一個等式________________;
(3)若![]() ,
,![]() .
.
①求![]() 的值。
的值。
②![]() ,
,![]() 的值.
的值.
【答案】(1)方法①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ②
②![]() 或
或![]() .
.
【解析】
(1)方法①根據(jù)陰影部分的面積=大正方形的面積-長方形的面積×4,即可解得;
方法②根據(jù)陰影部分的面積=小正方形的邊長×邊長,即可解答;
(2)根據(jù)(1)即可寫出等式;
(3)根據(jù)②的等式即可求出x-y的值.
解:(1)方法①:陰影部分的面積=(m+n)2﹣4mn;
方法②:陰影部分的面積=(m﹣n)2;
(2)由(1)得(m+n)2﹣4mn=(m﹣n)2,
(3)①由(2)可得:(x﹣y)2=(x+y)2﹣4xy,
∵![]() ,
,![]() ,
,
∴(x﹣y)2=36﹣11=25,
②∵(x﹣y)2=25,
∴x﹣y=±5.
∵![]() ,
,
∴![]() 或
或![]() ,
,
解之得
![]() 或
或![]() .
.


 世紀(jì)百通期末金卷系列答案
世紀(jì)百通期末金卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
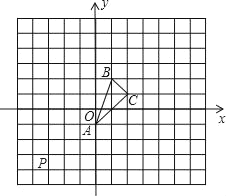
【題目】如圖是網(wǎng)格圖,每個小正方形的邊長均為1.△ABC它在坐標(biāo)平面內(nèi)平移,得到△PEF,點A平移后落在點P的位置上.
(1)請你在圖中畫出△PEF,并寫出頂點P、E、F的坐標(biāo);
(2)說出△PEF是由△ABC分別經(jīng)過怎樣的平移得到的?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖(十九),用四個螺絲將四條不可彎曲的木條圍成一個木框,不計螺絲大小,其中相鄰兩螺絲的距離依序為2、3、4、6,且相鄰兩木條的夾角均可調(diào)整。若調(diào)整木條的夾角時不破壞此木框,則任兩螺絲的距離之最大值為何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,點O在邊AB上,以點O為圓心,OA為半徑的圓經(jīng)過點C,過點C作直線MN,使∠BCM=2∠A.
(1)判斷直線MN與⊙O的位置關(guān)系,并說明理由;
(2)若OA=4,∠BCM=60°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,如圖,拋物線與x軸交點坐標(biāo)為A(1,0),C(-3,0),
(1)若已知頂點坐標(biāo)D為(-1,4)或B點(0,3),選擇適當(dāng)方式求拋物線的解析式.
(2)若直線DH為拋物線的對稱軸,在(1)的基礎(chǔ)上,求線段DK的長度,并求△DBC的面積.
(3)將圖(2)中的對稱軸向左移動,交x軸于點p(m,0)(-3<m<-1),與線段BC、拋物線的交點分別為點K、Q,用含m的代數(shù)式表示QK的長度,并求出當(dāng)m為何值時,△BCQ的面積最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
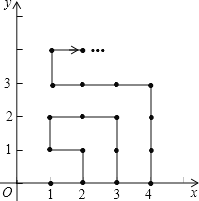
【題目】如圖,在平面直角坐標(biāo)系中,有若干個橫縱坐標(biāo)分別為整數(shù)的點,其順序按圖中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根據(jù)這個規(guī)律,第2019個點的坐標(biāo)為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖象分別與
的圖象分別與![]() 軸,
軸,![]() 軸交于
軸交于![]() ,以線段
,以線段![]() 為邊在第一象限內(nèi)作等腰直角三角形
為邊在第一象限內(nèi)作等腰直角三角形![]() ,使
,使![]() .
.
(1)分別求點![]() 的坐標(biāo);
的坐標(biāo);
(2)在![]() 軸上求一點
軸上求一點![]() ,使它到
,使它到![]() 兩點的距離之和最小.
兩點的距離之和最小.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com