
閱讀下列材料:
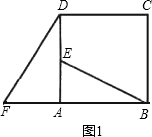
如圖1,在梯形ABCD中,AD∥BC,點M、N分別在邊AB、BC上,且MN∥AD,記AD=a,BC=b,若 ,則有結論:
,則有結論: 。
。

請根據以上結論,解答下列問題:

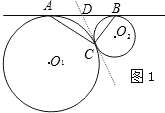
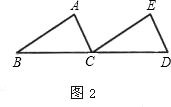
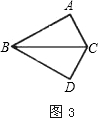
如圖2,3,BE、CF是△ABC的兩條角平分線,過EF上一點P分別作△ABC三邊的垂線段PP1、PP2、PP3,交BC于點P1,交AB于點P2,交AC于點P3。
(1)若點P為線段EF的中點,求證:PP1=PP2+PP3;
(2)若點P在線段EF上任意位置時,試探究PP1、PP2、PP3的數量關系,給出證明。
解:(1)證明:如圖,過點E作ED1⊥BC于D1,ED2⊥AB于D2,

∵BE是∠ABC的角平分線,∴ED1= ED2。
∵點P為線段EF的中點,且PP2⊥AB,
∴PP2∥ED2。∴ 。∴
。∴ ,即
,即 。
。
同理,過點F作FG1⊥BC于G1,FG2⊥AC于G2,得 。
。
在梯形EFG1D1中,∵公式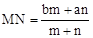 中,m=n,
中,m=n,
∴ (梯形中位線定理)。
(梯形中位線定理)。
∴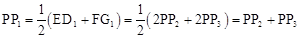 。
。
(2) 。證明如下:
。證明如下:
如圖,過點E作ED1⊥BC于D1,ED2⊥AB于D2,過點F作FG1⊥BC于G1,FG2⊥AC于G2,

設 ,則梯形EFG1D1滿足公式
,則梯形EFG1D1滿足公式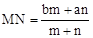 ,
,
∴ 。
。
公式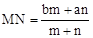 中,當b=0時,原梯形變為三角形,
中,當b=0時,原梯形變為三角形,
∴ 。
。
∴ 。
。
∴ ,
, 。
。
將②③代入①,得 。
。
【解析】(1)過點E作ED1⊥BC于D1,ED2⊥AB于D2,過點F作FG1⊥BC于G1,FG2⊥AC于G2,由角平分線上的點到角的兩邊距離相等,可得ED1= ED2,FG1= FG2。在△FED2和△FEG2中應用三角形中位線定理,可得 ,
, 。在梯形EFG1D1中,由公式可證得結論。
。在梯形EFG1D1中,由公式可證得結論。
(2)同(1)過點E作ED1⊥BC于D1,ED2⊥AB于D2,過點F作FG1⊥BC于G1,FG2⊥AC于G2,由角平分線上的點到角的兩邊距離相等,可得ED1= ED2,FG1= FG2。在△FED2、△FEG2和梯形EFG1D1中,由公式可求得結論。


科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
 閱讀下列材料:
閱讀下列材料: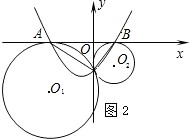
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| AM |
| MB |
| m |
| n |
| bm+an |
| m+n |

查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com