
【題目】已知拋物線![]()
(1)證明:不論m為何值,拋物線圖象的頂點(diǎn)![]() 均在某一直線
均在某一直線![]() 的圖象上,求此直線
的圖象上,求此直線![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)當(dāng)![]() 時(shí),點(diǎn)P為拋物線上一點(diǎn),且
時(shí),點(diǎn)P為拋物線上一點(diǎn),且![]() ,求點(diǎn)P的坐標(biāo);
,求點(diǎn)P的坐標(biāo);
(3)將(2)中的拋物線![]() 沿x軸翻折再向上平移1個(gè)單位向右平移
沿x軸翻折再向上平移1個(gè)單位向右平移![]() 個(gè)單位得拋物線
個(gè)單位得拋物線![]() ,設(shè)拋物線
,設(shè)拋物線![]() 的頂點(diǎn)為
的頂點(diǎn)為![]() ,拋物線
,拋物線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() (A在B的左邊),且
(A在B的左邊),且![]() ∥
∥![]() ,求
,求![]() 的值.
的值.
【答案】(1)證明見(jiàn)解析;(2)![]() (3)
(3)![]()
【解析】試題分析:(1)利用配方法可確定拋物線的頂點(diǎn)M坐標(biāo)為(m-1,-m-2),然后令x=m-1,y=-m-2,然后消去m得到x和y的關(guān)系式即可;
(2)先確定拋物線解析式為y=x2-2x-3,點(diǎn)M的坐標(biāo)為(1,-4),利用旋轉(zhuǎn)的定義,將線段OM繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得線段OC,與拋物線相交于點(diǎn)P,如圖1,從而得到點(diǎn)C坐標(biāo),再求出直線OP的解析式為y=![]() x,然后解方程組
x,然后解方程組 得P點(diǎn)坐標(biāo);
得P點(diǎn)坐標(biāo);
(3)利用拋物線的幾何變換得到N(n+1,5),拋物線C2的解析式為y=-(x-n-1)2+5,過(guò)點(diǎn)M作ME⊥x軸于點(diǎn)E,過(guò)點(diǎn)N作NF⊥x軸于點(diǎn)F,如圖2,根據(jù)拋物線與x軸的交點(diǎn)問(wèn)題求出A點(diǎn)和B點(diǎn)坐標(biāo),然后證明Rt△AME∽Rt△BNF,再利用相似比得到關(guān)于n的方程,解方程可得到n的值.
試題解析:(1)證明:y=x2-2(m-1)x+m2-3m-1=[x-(m-1)]2-m-2,則拋物線的頂點(diǎn)M坐標(biāo)為(m-1,-m-2),
令x=m-1,y=-m-2,
則x+y=-3,
所以直線l的函數(shù)解析式為y=-x-3;
(2)當(dāng)m=2時(shí),拋物線解析式為y=x2-2x-3,點(diǎn)M的坐標(biāo)為(1,-4),
將線段OM繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得線段OC,與拋物線相交于點(diǎn)P,如圖1,

則點(diǎn)C坐標(biāo)為(4,1),設(shè)直線OC的解析式為y=kx,
把C(4,1)代入得4k=1,解得k=![]() ,
,
所以直線OP的解析式為y=![]() x,
x,
解方程組 得
得 或
或 ,
,
所以點(diǎn)P的坐標(biāo)為(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)由題意可知,拋物線C2的頂點(diǎn)N(n+1,5),則拋物線C2的解析式為y=-(x-n-1)2+5,
過(guò)點(diǎn)M作ME⊥x軸于點(diǎn)E,過(guò)點(diǎn)N作NF⊥x軸于點(diǎn)F,如圖2,

當(dāng)y=0時(shí),-(x-n-1)2+5=0,解得x1=n+1-![]() ,x2=n+1+
,x2=n+1+![]() ,
,
∴A(n+1-![]() ,0),B(n+1+
,0),B(n+1+![]() ,0),
,0),
∵AM∥BN,
∴∠MAE=∠NBF,
∴Rt△AME∽Rt△BNF,
∴![]() ,即
,即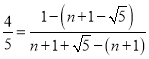 ,
,
∴n=![]() .
.


 陽(yáng)光試卷單元測(cè)試卷系列答案
陽(yáng)光試卷單元測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】探究:如圖①,在ABCD中,AC,BD交于點(diǎn)O,過(guò)點(diǎn)O的直線交AD于E,交BC于F.
(1)求證:OE=OF.
(2)求證:四邊形AEFB與四邊形DEFC的周長(zhǎng)相等;
(3)直線EF是否將ABCD的面積二等分?
應(yīng)用:張大爺家有一塊平行四邊形的菜園,園中有一口水井P,如圖②所示,張大爺計(jì)劃把菜園平均分成兩塊,分別種植西紅柿和茄子,且使兩塊地共用這口水井,請(qǐng)你幫助張大爺把地分開(kāi).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】李老師家距學(xué)校1 900 m,某天他步行去上班,走到路程的一半時(shí)發(fā)現(xiàn)忘帶手機(jī),此時(shí)離上班時(shí)間還有23 min,于是他立刻步行回家取手機(jī),隨后騎電瓶車(chē)返回學(xué)校.已知李老師騎電瓶車(chē)到學(xué)校比他步行到學(xué)校少用20 min,且騎電瓶車(chē)的平均速度是步行平均速度的5倍,李老師到家開(kāi)門(mén)、取手機(jī)、啟動(dòng)電瓶車(chē)等共用4 min.
(1)求李老師步行的平均速度;
(2)請(qǐng)你判斷李老師能否按時(shí)上班,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有20道競(jìng)賽題,對(duì)于每道題,答對(duì)得6分,答錯(cuò)或不答扣3分.小明在這次競(jìng)賽中的得分不少于80分,但又不多于90分,則小明答對(duì)的題數(shù)是( )道.
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】要了解全校學(xué)生的課外作業(yè)負(fù)擔(dān)情況,你認(rèn)為以下抽樣方法中比較合理的是( )
A.調(diào)查九年級(jí)全體學(xué)生
B.調(diào)查七、八、九年級(jí)各30名學(xué)生
C.調(diào)查全體女生
D.調(diào)查全體男生
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖, ![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
, ![]() ,反比例函數(shù)
,反比例函數(shù)![]() 與OA、AB分別相交于點(diǎn)D、C,且點(diǎn)D為OA的中點(diǎn),
與OA、AB分別相交于點(diǎn)D、C,且點(diǎn)D為OA的中點(diǎn),
(1)求反比例函數(shù)的解析式
(2)過(guò)點(diǎn)B的直線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 圖象交于第三象限內(nèi)一點(diǎn)F,求四邊形
圖象交于第三象限內(nèi)一點(diǎn)F,求四邊形![]() 的面積
的面積

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】矩形ABCD中,AB=10,BC=3,E為AB邊的中點(diǎn),P為CD邊上的點(diǎn),且△AEP是腰長(zhǎng)為5的等腰三角形,則DP=_____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形ABCD中,對(duì)角線AC上有一點(diǎn)P,連接BP、DP,過(guò)點(diǎn)P作PE⊥PB交CD于點(diǎn)E,連接BE.
(1)求證:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度數(shù);
(3)探究AP、PC、BE之間的數(shù)量關(guān)系,并給予證明.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com