
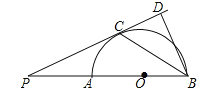
【題目】如圖,AB是半圓O的直徑,點P是BA延長線上一點,PC是⊙O的切線,切點為C,過點B作BD⊥PC交PC的延長線于點D,連接BC.求證:
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
試題分析:(1)連接OC,由PC為圓O的切線,利用切線的性質得到OC垂直于PC,再由BD垂直于PD,得到一對直角相等,利用同位角相等兩直線平行得到OC與BD平行,進而得到一對內錯角相等,再由OB=OC,利用等邊對等角得到一對角相等,等量代換即可得證;
(2)連接AC,由AB為圓O的直徑,利用圓周角定理得到∠ACB為直角,利用兩對角相等的三角形相似得到三角形ABC與三角形CBD相似,利用相似三角形對應邊成比例,變形即可得證.
試題解析:(1)連接OC,∵PC與圓O相切,∴OC⊥PC,即∠OCP=90°,∵BD⊥PD,∴∠BDP=90°,∴∠OCP=∠PDB,∴OC∥BD,∴∠BCO=∠CBD,∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD;
(2)連接AC,∵AB為圓O的直徑,∴∠ACB=90°,∴∠ACB=∠CDB=90°,∵∠ABC=∠CBD,∴△ABC∽△CBD,∴![]() ,則
,則![]() =ABBD.
=ABBD.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列結論:①若三角形一邊上的中線和這邊上的高重合,則這個三角形是等腰三角形;②近似數3.1416的精確度是千分位;③三邊分別為![]() 、
、![]() 、
、![]() 的三角形是直角三角形;④大于-
的三角形是直角三角形;④大于-![]() 而小于
而小于![]() 的所有整數的和為-4 ;⑤若一個直角三角形的兩邊長分別為3和4,則第三邊長是5; 其中正確的結論是______________(填序號);
的所有整數的和為-4 ;⑤若一個直角三角形的兩邊長分別為3和4,則第三邊長是5; 其中正確的結論是______________(填序號);
查看答案和解析>>
科目:初中數學 來源: 題型:
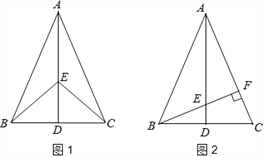
【題目】如圖1,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.
(1)求證:BE=CE;
(2)如圖2,若BE的延長線交AC于點F,且BF⊥AC,垂足為F,∠BAC=45°,原題設其它條件不變.求證:△AEF≌△BCF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com