
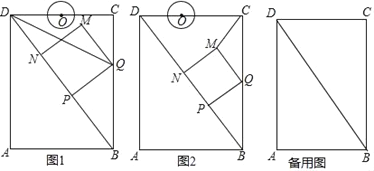
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點B出發,沿對角線BD向點D勻速運動,速度為4cm/s,過點P作PQ⊥BD交BC于點Q,以PQ為一邊作正方形PQMN,使得點N落在射線PD上.點O從點D出發,沿DC向點C勻速運動,速度為3cm/s,以O為圓心,1cm半徑作⊙O.點P與點D同時出發,設它們的運動時間為t(單位:s) (0≤t≤![]() ).
).
(1)如圖1,連接DQ,若DQ平分∠BDC,則t的值為 s;
(2)如圖2,連接CM,設△CMQ的面積為S,求S關于t的函數關系式;
(3)在運動過程中,當t為何值時,⊙O與MN第一次相切?
【答案】(1)1s; (2)S=﹣![]() t2+
t2+![]() t;(3)
t;(3)![]() .
.
【解析】試題分析:(1)由△DQC≌△DQP,推出DP=DC=6,在Rt△ADB中,BD=10,推出PB=4即可解決問題;
(2)過點M作MH⊥BC于點H,證明△HMQ∽△PQB,,由![]() =
=![]() ,得MH=
,得MH=![]() t,即可求得△CMQ的面積;
t,即可求得△CMQ的面積;
(3)設⊙O與MN相切于點E,連接OE,作OF⊥BD于點F,可證得△DFO∽△DCB,
由此![]() 即可解得:t值.
即可解得:t值.
試題解析:(1)∵四邊形ABCD為矩形,
∴AB=CD=6cm、AD=BC=8cm,
則DB=10cm,
∵四邊形PQMN為正方形,
∴∠BPQ=∠C=90°,
∵∠PBQ=∠CBD,
∴△BPQ∽△BCD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
則BQ=5t、PQ=3t,
∴CQ=BC﹣BQ=8﹣5t,
∵DQ平分∠BDC,
∴QP=QC,即3t=8﹣5t,
解得:t=1,
故答案為:1;
(2)如圖a,過點M作MH⊥BC于點H,
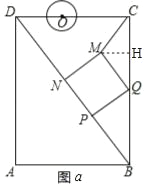
∴∠MHQ=∠QPB=∠MQP=90°,
則∠HMQ+∠HQM=∠PQB+∠HQM=90°,
∴∠HMQ=∠PQB,
∴△HMQ∽△PQB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
則MH=![]() t,
t,
∴S=![]() ×(8﹣5t)
×(8﹣5t)![]() t=﹣
t=﹣![]() t2+
t2+![]() t;
t;
(3)如圖b,設⊙O與MN相切于點E,連接OE,作OF⊥BD于點F,
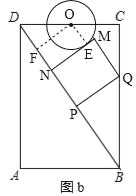
則四邊形OENF為矩形,
∴OE=FN=1,∠DFO=∠C=90°,
∵∠FDO=∠CDB,
∴△DFO∽△DCB,
∴![]() ,即
,即![]() ,
,
解得:t=![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A. 方程5x2=x有兩個不相等的實數根
B. 方程x2﹣8=0有兩個相等的實數根
C. 方程2x2﹣3x+2=0有兩個整數根
D. 當k>![]() 時,方程(k﹣1)x2+2x﹣3=0有兩個不相等的實數根
時,方程(k﹣1)x2+2x﹣3=0有兩個不相等的實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對平面直角坐標系中的點P(x,y),定義d=|x|+|y|,我們稱d為P(x,y)的幸福指數.對于函數圖象上任意一點P(x,y),若它的幸福指數d≥1恒成立,則稱此函數為幸福函數,如二次函數y=x2+1就是一個幸福函數,理由如下:設P(x,y)為y=x2+1上任意一點,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一個幸福函數.
(1)若點P在反比例函數y=![]() 的圖象上,且它的幸福指數d=2,請直接寫出所有滿足條件的P點坐標;
的圖象上,且它的幸福指數d=2,請直接寫出所有滿足條件的P點坐標;
(2)一次函數y=﹣x+1是幸福函數嗎?請判斷并說明理由;
(3)若二次函數y=x2﹣(2m+1)x+m2+m(m>0)是幸福函數,試求出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() ,
,![]() 平分
平分![]() ,點
,點![]() 在射線
在射線![]() 上,
上,![]() 、
、![]() 分別是射線
分別是射線![]() 、
、![]() 上的動點(
上的動點(![]() 、
、![]() 不與點
不與點![]() 重合),連接
重合),連接![]() 交射線
交射線![]() 于點
于點![]() .設
.設![]() .
.

(1)如圖1,若![]() ,則:①
,則:①![]() ______;②當
______;②當![]() 時,
時,![]() ______
______![]() .
.
(2)如圖2,若![]() ,垂足為
,垂足為![]() ,則是否存在這樣的
,則是否存在這樣的![]() 的值,使得
的值,使得![]() 中存在兩個相等的角?若存在,求出
中存在兩個相等的角?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,AB=4.作BM平分∠ABC交AC于點M,點D為射線BM上一點,以點B為旋轉中心將線段BD逆時針旋轉60°得到線段BE,連接DE.交射線BA于點F,連接AD、AE.當以A、D、M為頂點的三角形與△AEF全等時,DE的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
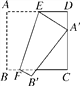
【題目】如圖,正方形紙片ABCD的邊長為12,E,F分別是邊AD,BC上的點,將正方形紙片沿EF折疊,使得點A落在CD邊上的點A′處,此時點B落在點B′處.已知折痕EF=13,則AE的長等于_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動——探究特殊的平行四邊形.
問題情境
如圖,在四邊形ABCD中,AC為對角線,AB=AD,BC=DC.請你添加條件,使它們成為特殊的平行四邊形.

提出問題
(1)第一小組添加的條件是“AB∥CD”,則四邊形ABCD是菱形.請你證明;
(2)第二小組添加的條件是“∠B=90°,∠BCD=90°”,則四邊形ABCD是正方形.請你證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:相等的實數看作同一個實數.有下列六種說法:
①數軸上有無數多個表示無理數的點;
②帶根號的數不一定是無理數;
③每個有理數都可以用數軸上唯一的點來表示;
④數軸上每一個點都表示唯一一個實數;
⑤沒有最大的負實數,但有最小的正實數;
⑥沒有最大的正整數,但有最小的正整數.
其中說法錯誤的有_____(注:填寫出所有錯誤說法的編號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店準備購進A、B兩種型號的書包共50個進行銷售,兩種書包的進價、售價如下表所示:
書包型號 | 進價(元/個) | 售價(元/個) |
A型 | 200 | 300 |
B型 | 100 | 150 |
購進這50個書包的總費用不超過7300元,且購進B型書包的個數不大于A型書包個數的![]() .
.
(1)該文具店有哪幾種進貨方案?
(2)若該文具店購進的50個書包全部售完,則該文具店采用哪種進貨方案,才能獲得最大利潤?最大利潤是多少?(利潤=售價﹣進價)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com