
【題目】如圖,是一塊含30°(即∠CAB=30°)角的三角板和一個量角器拼在一起,三角板斜邊AB與量角器所在圓的直徑MN恰好重合,其量角器最外緣的讀數是從N點開始(即N點的讀數為0°),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E.

(1)當旋轉7.5秒時,連接BE,試說明:BE=CE;
(2)填空:①當射線CP經過△ABC的外心時,點E處的讀數是 .
②當射線CP經過△ABC的內心時,點E處的讀數是 ;
③設旋轉x秒后,E點出的讀數為y度,則y與x的函數式是y= .
【答案】(1)見解析;(2)①120°;②90°;③y=180﹣4x
【解析】
(1)由于是每次都旋轉2°且CP的旋轉決定著∠ACE和∠ABE,且二者都是從0°開始的,所以:∠ACE=∠ABE,只要證明:∠CBE=∠BCE即可證明BE=CE;
(2)①當射線CP經過△ABC的外心時,CP經過AB的中心且此時有:CO=AO,可以得出∠OCA=∠CAB=30°,即可求出點E處的度數;
②當射線CP經過△ABC的內心時,內心到三邊的距離相等,即CP為∠ACB的角平分線,所以有∠ABE=∠ACE=45°,即可求出點E處的度數;
③由于每次旋轉的度數一樣,所以旋轉x秒后,∠BCE的度數為90°﹣2x,從而得出∠BOE的度數,也即可得出y與x的函數式.
(1)證明:連接BE,如圖所示:
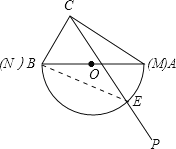
∵射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉
∴當旋轉7.5秒時,∠ACE=7.5×2°=∠ABE=15°
又∵∠CAB=30°,∠CBA=60°,∠ACB=90°
∴∠CBE=75°,∠BCE=90°﹣15°=75°,
即:∠CBE=∠BCE=75°
∴BE=CE.
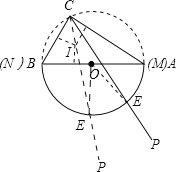
(2)解:①當射線CP經過△ABC的外心時,CP經過AB的中點且此時有:CO=AO;
∴∠OCA=∠CAB=30°,∠AOE=60°
∴點E處的讀數是120°.
②當射線CP經過△ABC的內心時,即CP為∠ACB的角平分線,
圓周角∠BCE=![]() =45°,圓心角為90°,
=45°,圓心角為90°,
∴點E處的讀數是90°.
③旋轉x秒后,∠BCE的度數為90﹣2x,∠BOE的度數為180°﹣4x,
故可得y與x的函數式為:y=180°﹣4x.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
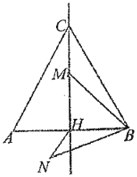
【題目】如圖,等邊三角形![]() 的邊長是2,
的邊長是2,![]() 是高
是高![]() 所在直線上的一個動點,連接
所在直線上的一個動點,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,連接
,連接![]() ,則在點
,則在點![]() 運動過程中,線段
運動過程中,線段![]() 長度的最小值是( )
長度的最小值是( )
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如今很多初中生喜歡購頭飲品飲用,既影響身體健康又給家庭增加不必要的開銷,為此某班數學興趣小組對本班同學一天飲用飲品的情況進行了調查,大致可分為四種:A.白開水,B.瓶裝礦泉水,C.碳酸飲料,D.非碳酸飲料.根據統計結果繪制如下兩個統計圖,根據統計圖提供的信息,解答下列問題
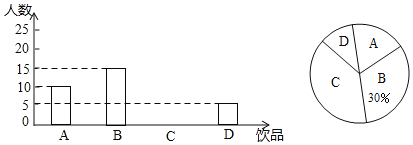
(1)這個班級有多少名同學?并補全條形統計圖;
(2)若該班同學每人每天只飲用一種飲品(每種僅限一瓶,價格如下表),則該班同學每天用于飲品的人均花費是多少元?
飲品名稱 | 白開水 | 瓶裝礦泉水 | 碳酸飲料 | 非碳酸飲料 |
平均價格(元/瓶) | 0 | 2 | 3 | 4 |
(3)為了養成良好的生活習慣,班主任決定在飲用白開水的5名班委干部(其中有兩位班長記為A,B,其余三位記為C,D,E)中隨機抽取2名班委干部作良好習慣監督員,請用列表法或畫樹狀圖的方法求出恰好抽到2名班長的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,先將正方形紙片兒對折,折痕為MN,再把點B折疊在折痕MN上,折痕為AE,點E在CB上,點B在MN上的對應點為H,沿AH和DH剪下得到三角形ADH,則下列選項錯誤的是( )
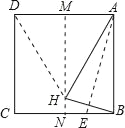
A. DH=AD B. AH=DH C. NE=BE D. DM=![]() DH
DH
查看答案和解析>>
科目:初中數學 來源: 題型:
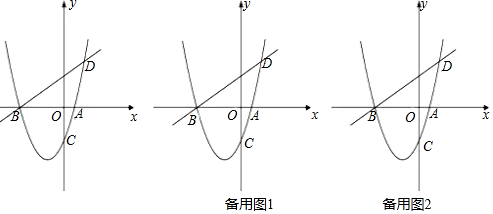
【題目】如圖,已知拋物線![]() 與x軸交于A、B兩點,與y軸交于C點,直線BD交拋物線于點D,并且
與x軸交于A、B兩點,與y軸交于C點,直線BD交拋物線于點D,并且![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)已知點M為拋物線上一動點,且在第三象限,順次連接點B、M、C,求![]() 面積的最大值;
面積的最大值;
(3)在(2)中![]() 面積最大的條件下,過點M作直線平行于y軸,在這條直線上是否存在一個以Q點為圓心,OQ為半徑且與直線AC相切的圓?若存在,求出圓心Q的坐標;若不存在,請說明理由.
面積最大的條件下,過點M作直線平行于y軸,在這條直線上是否存在一個以Q點為圓心,OQ為半徑且與直線AC相切的圓?若存在,求出圓心Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
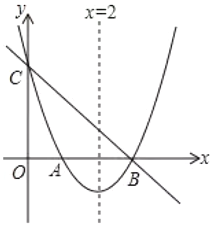
【題目】如圖,直線y= -x+3與x軸,y軸分別相交于點B、C,經過B、C兩點的拋物線![]() 與x軸的另一交點為A,頂點為P,且對稱軸為直線x=2.
與x軸的另一交點為A,頂點為P,且對稱軸為直線x=2.
(1)求A點的坐標;
(2)求該拋物線的函數表達式;
(3)連結AC.請問在x軸上是否存在點Q,使得以點P、B、Q為頂點的三角形與△ABC 相似,若存在,請求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com