
【題目】(問題背景)如圖1所示,在![]() 中,
中,![]() ,
,![]() ,點D為直線
,點D為直線![]() 上的個動點(不與B、C重合),連結
上的個動點(不與B、C重合),連結![]() ,將線段
,將線段![]() 繞點D按順時針方向旋轉90°,使點A旋轉到點E,連結
繞點D按順時針方向旋轉90°,使點A旋轉到點E,連結![]() .
.
(問題初探)如果點D在線段![]() 上運動,通過觀察、交流,小明形成了以下的解題思路:過點E作
上運動,通過觀察、交流,小明形成了以下的解題思路:過點E作![]() 交直線
交直線![]() 于F,如圖2所示,通過證明
于F,如圖2所示,通過證明![]() ______,可推證
______,可推證![]() 是_____三角形,從而求得
是_____三角形,從而求得![]() ______°.
______°.
(繼續探究)如果點D在線段![]() 的延長線上運動,如圖3所示,求出
的延長線上運動,如圖3所示,求出![]() 的度數.
的度數.
(拓展延伸)連接![]() ,當點D在直線
,當點D在直線![]() 上運動時,若
上運動時,若![]() ,請直接寫出
,請直接寫出![]() 的最小值.
的最小值.
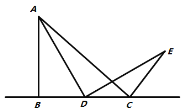
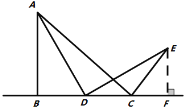
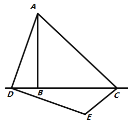
圖1 圖2 圖3
【答案】(1)△ADB,等腰直角,135°;(2)45°;(3)![]() .
.
【解析】
(1)問題初探:由旋轉的性質得到∠ADE=90°,AD=DE,則∠ADB+∠EDF=∠ADB+∠DAB=90°,得到∠DAB=∠EDF,則根據AAS得到△DEF≌△ADB;則EF=BD,DF=AB,則AB=AC=DF,得到BD=CF=EF,則△CEF是等腰直角三角形;從而得到∠DCE=135°;
(2)繼續探究:過點E作EG⊥CD,與(1)同理,可證△ABD≌△DGE,得到BD=GE,AB=DG=BC,則BD=CG=GE,即可得到![]() ;
;
(3)拓展延伸:當點D在直線BC上運動時,當BE⊥CE時,BE的長度是最小值,由(2)可知![]() ,則△BCE為等腰直角三角形,則
,則△BCE為等腰直角三角形,則![]() .
.
解:(1)問題初探:如圖,
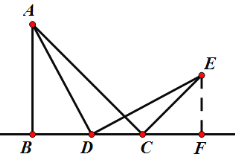
由旋轉的性質,得:∠ADE=90°,AD=DE,
∴∠ADB+∠EDF=90°,
∵∠ABC=90°,
∴∠ADB+∠DAB=90°,
∴∠DAB=∠EDF,
∵EF⊥BC,
∴∠ABC=∠DFE=90°,
∴△ADB≌△DEF(AAS);
∴BD=EF,AB=DF,
∴AB=DF=BC,
∴BD+DC=DC+CF,
∴BD=CF=EF,
∴△CEF是等腰直角三角形;
∴∠CEF=45°,
∴∠DCE=∠CEF+∠CFE=45°+90°=135°;
故答案為:△ADB,等腰直角,135°;
(2)繼續探究:如圖,過點E作EG⊥CD,
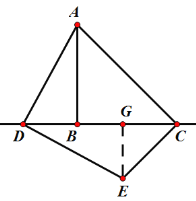
∵∠ADE=∠ADB+∠GDE=90°,∠ADB+∠DAB=90°,
∴∠GDE=∠DAB,
∵∠ABD=∠DGE=90°,AD=DE,
∴△ABD≌△DGE(AAS),
∴BD=GE,AB=DG=BC,
∴BD+BG=BG+GC,
∴CG=BD=GE,
∴△CEG是等腰直角三角形,
∴∠DCE=45°;
(3)拓展延伸:如圖,當點D在直線BC上運動時,當BE⊥CE時,BE的長度是最小值;
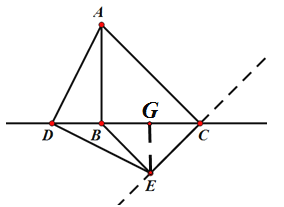
則∠BEC=90°.
由(2)可知,∠DCE=45°,
∴△BCE是等腰直角三角形,
∴BE=CE,
∵![]() ,
,
∴![]() ;
;
∴BE的最小值為![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D在△ABC內,BD=BC,∠DBC=60°,點E在△ABC外,∠BCE=150°,∠ABE=60°.
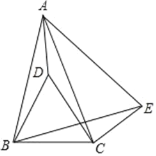
(1)求證:△ADB≌△ADC , 并求出∠ADB的度數;
(2)小明說△ABE是等腰三角形,小華說△ABE是等邊三角形.請問 說法更準確,并說明理由.
(3)連接DE,若DE⊥BD,DE=8,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
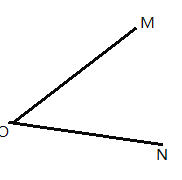
【題目】如圖,已知![]() .
.
(1)用直尺和圓規畫出![]() 的平分線
的平分線![]() (保留作圖痕跡,不寫作法,不用證明)
(保留作圖痕跡,不寫作法,不用證明)
(2)在射線![]() 上任意選取一點
上任意選取一點![]() ,再在射線
,再在射線![]() 上選取一點
上選取一點![]() ,要求
,要求![]() 為鈍角.
為鈍角.
①在射線![]() 上找到所有使得
上找到所有使得![]() 的點
的點![]() .
.
②寫出![]() 與
與![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
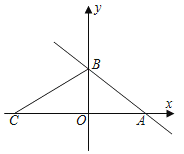
【題目】如圖,一次函數y=﹣![]() x+3的圖象與x軸交于點A,與y軸交于點B,C是x軸上一動點,連接BC,將△ABC沿BC所在的直線折疊,當點A落在y軸上時,點C的坐標為__.
x+3的圖象與x軸交于點A,與y軸交于點B,C是x軸上一動點,連接BC,將△ABC沿BC所在的直線折疊,當點A落在y軸上時,點C的坐標為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
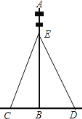
【題目】如圖,為了使電線桿穩固的垂直于地面,兩側常用拉緊的鋼絲繩索固定,由于鋼絲繩的交點![]() 在電線桿的上三分之一處,所以知道
在電線桿的上三分之一處,所以知道![]() 的高度就可以知道電線桿
的高度就可以知道電線桿![]() 的高度了.要想得到
的高度了.要想得到![]() 的高度,需要測量出一些數據,然后通過計算得出.
的高度,需要測量出一些數據,然后通過計算得出.
請你設計出要測量的對象:________;
請你寫出計算![]() 高度的思路:________.
高度的思路:________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 同時滿足下列條件:對稱軸是
同時滿足下列條件:對稱軸是![]() ;最值是
;最值是![]() ;二次函數的圖象與
;二次函數的圖象與![]() 軸有兩個交點,其橫坐標的平方和為
軸有兩個交點,其橫坐標的平方和為![]() ,則
,則![]() 的值是( )
的值是( )
A. ![]() 或
或![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】任意兩點關于它們所連線段的中點成中心對稱,在平面直角坐標系中,任意兩點P(x1,y1),Q (x2,y2)的對稱中心的坐標為![]() ,如圖.
,如圖.
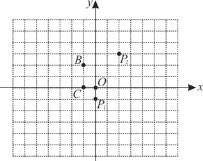
(1)在平面直角坐標系中,若點P1(0,-1),P2(2,3)的對稱中心是點A,則點A的坐標為________;
(2)另取兩點![]() ,
,![]() .有一電子青蛙從點P1處開始依次作關于點A,B,C的循環對稱跳動,即第一次跳到點P1關于點A的對稱點P2處,接著跳到點P2關于點B的對稱點P3處,第三次再跳到點P3關于點C的對稱點P4處,第四次再跳到點P4關于點A的對稱點P5處,…,則點
.有一電子青蛙從點P1處開始依次作關于點A,B,C的循環對稱跳動,即第一次跳到點P1關于點A的對稱點P2處,接著跳到點P2關于點B的對稱點P3處,第三次再跳到點P3關于點C的對稱點P4處,第四次再跳到點P4關于點A的對稱點P5處,…,則點![]() 的坐標為________.
的坐標為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在![]() 中,
中,![]() .
.
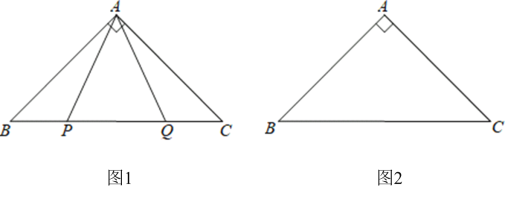
(1)如圖1,![]() 是
是![]() 邊上兩點,
邊上兩點,![]() , 求
, 求![]() 的度數.
的度數.
(2)點![]() 是
是![]() 邊上兩動點(不與
邊上兩動點(不與![]() 重合), 點
重合), 點![]() 在點
在點![]() 左側,且
左側,且![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
①依題意將圖2補全.
②小明通過觀察和實驗,提出猜想:在點![]() 運動的過程中,始終有
運動的過程中,始終有![]() 為等腰直角三角形,他把這個猜想與同學們進行交流,通過討論,形成以下證明猜想的思路:要想證明
為等腰直角三角形,他把這個猜想與同學們進行交流,通過討論,形成以下證明猜想的思路:要想證明![]() 為等腰直角三角形,只需證
為等腰直角三角形,只需證![]() .
.
請參考上面的思路,幫助小明證明△APM 為等腰直角三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com