
【題目】在平面直角坐標(biāo)系中,點(diǎn) B(m,n) 在第一象限,m,n 均為整數(shù),且滿足n =![]() .
.
(1) 求點(diǎn) B 的坐標(biāo);
(2) 將線段 OB 向下平移 a 個單位后得到線段 O′B′,過點(diǎn) B′作 B′C⊥y 軸于點(diǎn) C,若 3CO=2CO′,求a 的值;
(3) 過點(diǎn) B 作與 y 軸平行的直線 BM,點(diǎn) D 在 x 軸上,點(diǎn) E 在 BM 上,點(diǎn) D 從 O 點(diǎn)出發(fā)以每秒鐘 3個單位長度的速度沿 x 軸向右運(yùn)動,同時點(diǎn) E 從 B 點(diǎn)出發(fā)以每秒鐘 2 個單位長度的速度沿BM 向下運(yùn)動,在點(diǎn) D,E 運(yùn)動的過程中,若直線 OE,BD 相交于點(diǎn) G,且 5≤S△OGB≤10,則點(diǎn)G 的橫坐標(biāo) xG的取值范圍是 .
【答案】(1)B的坐標(biāo)(3,2) ;(2)![]() ,
,![]() ; (3) 4≤xG≤
; (3) 4≤xG≤![]() .
.
【解析】(1)由點(diǎn)![]() 在第一象限可得
在第一象限可得 ![]() ,由n =
,由n =![]() 可得
可得![]() ,結(jié)合m,n 均為整數(shù),可求出m,n的值;
,結(jié)合m,n 均為整數(shù),可求出m,n的值;
(2)根據(jù)平移的性質(zhì),分當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 上方時和當(dāng)點(diǎn)
上方時和當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 之間時兩種情況求解即可;
之間時兩種情況求解即可;
(3)設(shè)t秒后5≤S△OGB≤10,則D(3t,0),E(3,2-2t),則可求直線BD的解析式為![]() ,直線OE的解析式為
,直線OE的解析式為![]() ,聯(lián)立后求出點(diǎn)G的坐標(biāo),然后根據(jù)三角形的面積公式列式計(jì)算即可.
,聯(lián)立后求出點(diǎn)G的坐標(biāo),然后根據(jù)三角形的面積公式列式計(jì)算即可.
(1)∵ 點(diǎn)![]() 在第一象限,
在第一象限,
∴ ![]() ,
,
依題意可知,![]() ,
,
∴ ![]() .
.
∵ ![]() 為整數(shù),
為整數(shù),
∴ ![]() 或
或![]() 或
或![]() ,
,
當(dāng)![]() ,
,![]() 時,n的值都不合題意舍去;
時,n的值都不合題意舍去;
當(dāng)![]() 時,
時,![]() ,
,
∴ 點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ;
;
(2) ① 如圖,當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 上方時
上方時
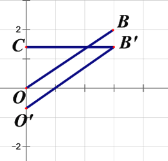
![]() , ∴
, ∴![]() ,
,![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ;
;
② 如圖,當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 之間時
之間時
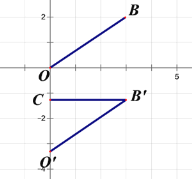
同理可求![]() .
.
(3)4≤xG≤![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】
![]()
(1)OA= cm,OB= cm.
(2)若點(diǎn)C是線段AO上一點(diǎn),且滿足AC=CO+CB,求CO的長.
(3)若動點(diǎn)P、Q分別從A、B同時出發(fā),向右運(yùn)動,點(diǎn)P的速度為2cm/s,點(diǎn)Q的速度為1cm/s,設(shè)運(yùn)動時間為t(s),當(dāng)點(diǎn)P與點(diǎn)Q重合時,P、Q兩點(diǎn)停止運(yùn)動.
①當(dāng)t為何值時,2OP﹣OQ=8.
②當(dāng)點(diǎn)P經(jīng)過點(diǎn)O時,動點(diǎn)M從點(diǎn)O出發(fā),以3cm/s的速度也向右運(yùn)動.當(dāng)點(diǎn)M追上點(diǎn)Q后立即返回,以同樣的速度向點(diǎn)P運(yùn)動,遇到點(diǎn)P后立即返回,又以同樣的速度向點(diǎn)Q運(yùn)動,如此往返,直到點(diǎn)P、Q停止時,點(diǎn)M也停止運(yùn)動.在此過程中,點(diǎn)M行駛的總路程為 cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知AB=AD,那么添加下列一個條件后,仍無法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,長方形ABCD中,AD=BC=6,AB=CD=4.點(diǎn)P從點(diǎn)A出發(fā),以每秒1個單位的速度沿A→B→C→D→A的方向運(yùn)動,回到點(diǎn)A停止運(yùn)動.設(shè)運(yùn)動時間為t秒.
(1)當(dāng)t= 時,點(diǎn)P到達(dá)點(diǎn)C;當(dāng)t= 時,點(diǎn)P回到點(diǎn)A;
(2)△ABP面積取最大值時t的取值范圍;(3)當(dāng)△ABP的面積為3時,求t的值;
(4)若點(diǎn)P出發(fā)時,點(diǎn)Q從點(diǎn)A出發(fā),以每秒2個單位的速度沿A→D→C→B→A的方向運(yùn)動,回到點(diǎn)A停止運(yùn)動.請問:P 、Q何時在長方形ABCD的邊上相距1個單位長度?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
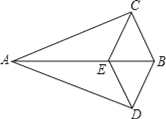
【題目】如圖,△ABC≌△ABD,點(diǎn)E在邊AB上,CE∥BD,連接DE.
求證:(1)∠CEB=∠CBE;
(2)四邊形BCED是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有一個長方形,若它的長增加 9cm,則變?yōu)閷挼膬杀叮蝗羲膶捲黾?/span> 5cm,則只比長少 1cm.
(1) 這個長方形的長和寬各是多少 cm?
(2) 將這個長方形的長減少 a cm,寬增加 b cm,使它變成一個正方形,若 a,b均為正整數(shù),所得正方形的周長不大于原長方形的周長,求這個正方形的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,對角線AC,BD相交于點(diǎn)O,DH⊥AB于點(diǎn)H,連接OH,求證:∠DHO=∠DCO.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,矩形OCDE的三個頂點(diǎn)分別是C(3,0),D(3,4),E(0,4).點(diǎn)A在DE上,以A為頂點(diǎn)的拋物線過點(diǎn)C,且對稱軸x=1交x軸于點(diǎn)B.連接EC,AC.點(diǎn)P,Q為動點(diǎn),設(shè)運(yùn)動時間為t秒. 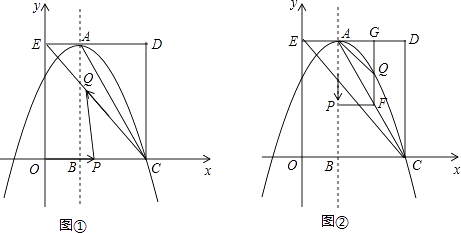
(1)填空:點(diǎn)A坐標(biāo)為;拋物線的解析式為 .
(2)在圖①中,若點(diǎn)P在線段OC上從點(diǎn)O向點(diǎn)C以1個單位/秒的速度運(yùn)動,同時,點(diǎn)Q在線段CE上從點(diǎn)C向點(diǎn)E以2個單位/秒的速度運(yùn)動,當(dāng)一個點(diǎn)到達(dá)終點(diǎn)時,另一個點(diǎn)隨之停止運(yùn)動.當(dāng)t為何值時,△PCQ為直角三角形?
(3)在圖②中,若點(diǎn)P在對稱軸上從點(diǎn)A開始向點(diǎn)B以1個單位/秒的速度運(yùn)動,過點(diǎn)P做PF⊥AB,交AC于點(diǎn)F,過點(diǎn)F作FG⊥AD于點(diǎn)G,交拋物線于點(diǎn)Q,連接AQ,CQ.當(dāng)t為何值時,△ACQ的面積最大?最大值是多少?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com