
【題目】在平面直角坐標系中 xOy 中,對于⊙C及⊙C內一點 P,給出如下定義:若存在過點 P 的直線 l,使得它與⊙C 相交所截得的弦長為![]() ,則稱點 P 為⊙C的“k-近內點”.
,則稱點 P 為⊙C的“k-近內點”.
(1)已知⊙O的半徑為 4,
①在點中![]() ,⊙O的“4-近內點”是______________;
,⊙O的“4-近內點”是______________;
②點 P 在直線y=![]() x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
(2)⊙C的圓心為(-1,0),半徑為 3,直線![]() x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2
x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2![]() -近內點”,則 b 的取值范圍是____________.
-近內點”,則 b 的取值范圍是____________.
【答案】(1)①P2,P3.; ②![]() 或
或![]() ;(2)
;(2)![]() 或
或![]()
【解析】
通過讀題,理解本題的實質強調兩點:
(1)確定點P在圓內,即點心距小于半徑.
(2)過點P的直線截圓所得的弦長可以取到k.即過圓內一點的直線截圓所得的弦的最小值應小于或等于k,數形結合,由弦長公式及其相關不等式結合來計算求解即可.
解:由于經過圓內一點的直線被圓所截的弦的長度的最大值為直徑,最小值是當直線垂直于經過該點的直徑時弦長最短.只有當最短的弦長不大于k值時,弦長才可能取到k.
(1)①OP1=2,r=4,由弦長公式得 最短弦長為![]() ,不滿足, OP2=
,不滿足, OP2=![]() ,r=4,由弦長公式得最短弦長為
,r=4,由弦長公式得最短弦長為![]() ,滿足,OP3=
,滿足,OP3=![]() ,r=4,由弦長公式得最短弦長
,r=4,由弦長公式得最短弦長![]() ,
,
滿足,所以⊙O的“4-近內點”是P2,P3.
②依題意:設P點的坐標為![]() ,則OP2=
,則OP2=![]() ,半徑r=4, 由弦長公式得最短弦長
,半徑r=4, 由弦長公式得最短弦長![]() 且OP2 =
且OP2 =![]() < r2=16, 即
< r2=16, 即
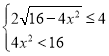
解得:![]() 或
或![]()
∵![]()
∴![]() 或
或![]() ,
,
(2)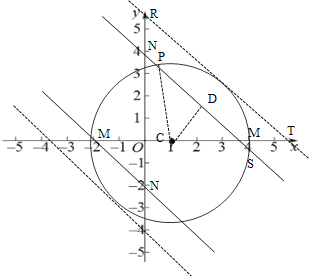
如圖所示,直線MN,過圓心C作CD⊥MN,若此時弦PS=2![]() ,∴PD=
,∴PD=![]() ,
,
連接PG,則PG=3,由勾股定理得GD=2,
又∵![]() 為等腰直角三角形
為等腰直角三角形
∴GM=2![]() ,
,
∴OM=ON=2![]() +1,
+1,
由(1)可知當直線MN向上平移到RT位置恰好與圓C相切時,GT=3![]() ,
,
∴OT=OR=3![]() +1,
+1,
∴![]()
由對稱性可知![]()
綜上,b的取值范圍為![]() 或
或![]()


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,OD⊥弦BC于點F,交⊙O于點E,連接CE,AE,CD,若∠AEC=∠ODC.
(1)求證:直線CD為⊙O的切線;
(2)若AB=10,BC=8,則線段CD的長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國正在逐步進入人口老齡化社會,某市老齡化社會研究機構經過抽樣調查,發現當地老年人的日常休閑方式主要有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五種類型,抽樣調查的統計結果如下表,則下列說法不正確的是( )
五種類型,抽樣調查的統計結果如下表,則下列說法不正確的是( )
休閑類型 | 休閑方式 | 人數 |
| 老年大學 |
|
| 老年合唱隊 |
|
| 老年舞蹈隊 |
|
| 太極拳 |
|
| 其它方式 |
|
A.當地老年人選擇![]() 型休閑方式的人數最少
型休閑方式的人數最少
B.當地老年人選擇![]() 型休閑方式的頻率是
型休閑方式的頻率是![]()
C.估計當地![]() 萬名老年人中約有
萬名老年人中約有![]() 萬人選擇
萬人選擇![]() 型休閑方式
型休閑方式
D.這次抽樣調查的樣本容量是![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,拋物線![]() 的頂點坐標為
的頂點坐標為![]() ,并與
,并與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是對稱軸與
是對稱軸與![]() 軸的交點.
軸的交點.
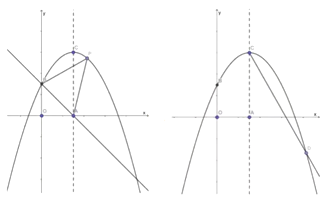
(1)求拋物線的解析式;
(2)如圖①所示, ![]() 是拋物線上的一個動點,且位于第一象限,連結BP、AP,求
是拋物線上的一個動點,且位于第一象限,連結BP、AP,求![]() 的面積的最大值;
的面積的最大值;
(3)如圖②所示,在對稱軸![]() 的右側作
的右側作![]() 交拋物線于點
交拋物線于點![]() ,求出
,求出![]() 點的坐標;并探究:在
點的坐標;并探究:在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 內接于⊙O,∠B=60°,CD 是⊙O 的直徑,點 P 是 CD 延長線上的一點且 AP=AC.

(1)求證:PA 是⊙O 的切線;
(2)若![]() ,
,![]() ,求⊙O的半徑
,求⊙O的半徑
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組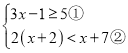
請結合題意,完成本題的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,支付方式的“眾數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
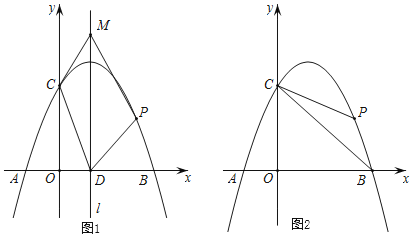
【題目】如圖1,已知拋物線y=﹣x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于C點,點P是拋物線上在第一象限內的一個動點,且點P的橫坐標為t.
(1)求拋物線的表達式;
(2)設拋物線的對稱軸為l,l與x軸的交點為D.在直線l上是否存在點M,使得四邊形CDPM是平行四邊形?若存在,求出點M的坐標;若不存在,請說明理由.
(3)如圖2,連接BC,PB,PC,設△PBC的面積為S.
①求S關于t的函數表達式;
②求P點到直線BC的距離的最大值,并求出此時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com