
【題目】如圖,在平面直角坐標系中,二次函數![]() 交
交![]() 軸于點
軸于點![]() 、
、![]() ,交
,交![]() 軸于點
軸于點![]() ,在
,在![]() 軸上有一點
軸上有一點![]() ,連接
,連接![]() .
.

(1)求二次函數的表達式;
(2)若點![]() 為拋物線在
為拋物線在![]() 軸負半軸上方的一個動點,求
軸負半軸上方的一個動點,求![]() 面積的最大值;
面積的最大值;
(3)拋物線對稱軸上是否存在點![]() ,使
,使![]() 為等腰三角形,若存在,請直接寫出所有
為等腰三角形,若存在,請直接寫出所有![]() 點的坐標,若不存在請說明理由.
點的坐標,若不存在請說明理由.
【答案】(1)二次函數的解析式為![]() ;(2)當
;(2)當![]() 時,
時,![]() 的面積取得最大值
的面積取得最大值![]() ;(3)
;(3)![]() 點的坐標為
點的坐標為![]() ,
,![]() ,
,![]() .
.
【解析】(1)把已知點坐標代入函數解析式,得出方程組求解即可;
(2)根據函數解析式設出點D坐標,過點D作DG⊥x軸,交AE于點F,表示△ADE的面積,運用二次函數分析最值即可;
(3)設出點P坐標,分PA=PE,PA=AE,PE=AE三種情況討論分析即可.
(1)∵二次函數y=ax2+bx+c經過點A(﹣4,0)、B(2,0),C(0,6),
∴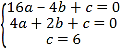 ,
,
解得: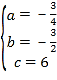 ,
,
所以二次函數的解析式為:y=![]() ;
;
(2)由A(﹣4,0),E(0,﹣2),可求AE所在直線解析式為y=![]() ,
,
過點D作DN⊥x軸,交AE于點F,交x軸于點G,過點E作EH⊥DF,垂足為H,如圖,
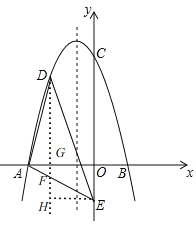
設D(m,![]() ),則點F(m,
),則點F(m,![]() ),
),
∴DF=![]() ﹣(
﹣(![]() )=
)=![]() ,
,
∴S△ADE=S△ADF+S△EDF=![]() ×DF×AG+
×DF×AG+![]() DF×EH
DF×EH
=![]() ×DF×AG+
×DF×AG+![]() ×DF×EH
×DF×EH
=![]() ×4×DF
×4×DF
=2×(![]() )
)
=![]() ,
,
∴當m=![]() 時,△ADE的面積取得最大值為
時,△ADE的面積取得最大值為![]() .
.
(3)y=![]() 的對稱軸為x=﹣1,設P(﹣1,n),又E(0,﹣2),A(﹣4,0),可求PA=
的對稱軸為x=﹣1,設P(﹣1,n),又E(0,﹣2),A(﹣4,0),可求PA=![]() ,PE=
,PE=![]() ,AE=
,AE=![]() ,分三種情況討論:
,分三種情況討論:
當PA=PE時,![]() =
=![]() ,解得:n=1,此時P(﹣1,1);
,解得:n=1,此時P(﹣1,1);
當PA=AE時,![]() =
=![]() ,解得:n=
,解得:n=![]() ,此時點P坐標為(﹣1,
,此時點P坐標為(﹣1,![]() );
);
當PE=AE時,![]() =
=![]() ,解得:n=﹣2
,解得:n=﹣2![]() ,此時點P坐標為:(﹣1,﹣2
,此時點P坐標為:(﹣1,﹣2![]() ).
).
綜上所述:P點的坐標為:(﹣1,1),(﹣1,![]() ),(﹣1,﹣2
),(﹣1,﹣2![]() ).
).


 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】閱讀材料:一般情形下等式![]() =1不成立,但有些特殊實數可以使它成立,例如:x=2,y=2時,
=1不成立,但有些特殊實數可以使它成立,例如:x=2,y=2時,![]() =1成立,我們稱(2,2)是使
=1成立,我們稱(2,2)是使![]() =1成立的“神奇數對”.請完成下列問題:
=1成立的“神奇數對”.請完成下列問題:
(1)數對(![]() ,4),(1,1)中,使
,4),(1,1)中,使![]() =1成立的“神奇數對”是 ;
=1成立的“神奇數對”是 ;
(2)若(5﹣t,5+t)是使![]() =1成立的“神奇數對”,求t的值;
=1成立的“神奇數對”,求t的值;
(3)若(m,n)是使![]() =1成立的“神奇數對”,且a=b+m,b=c+n,求代數式(a﹣c)2﹣12(a﹣b)(b﹣c)的最小值.
=1成立的“神奇數對”,且a=b+m,b=c+n,求代數式(a﹣c)2﹣12(a﹣b)(b﹣c)的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋一枚均勻硬幣正面朝上的概率為![]() ,下列說法錯誤的是
,下列說法錯誤的是
A. 連續拋一均勻硬幣2次必有1次正面朝上
B. 連續拋一均勻硬幣10次都可能正面朝上
C. 大量反復拋一均勻硬幣,平均100次出現正面朝上50次
D. 通過拋一均勻硬幣確定誰先發球的比賽規則是公平的
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 中,如果過項點
中,如果過項點![]() 的一條直線把這個三角形分割成兩個三角形,其中一個為等腰三角形,另一個為直角三角形,則稱這條直線為
的一條直線把這個三角形分割成兩個三角形,其中一個為等腰三角形,另一個為直角三角形,則稱這條直線為![]() 的關于點
的關于點![]() 的二分割線.例如:如圖1,
的二分割線.例如:如圖1,![]() 中,
中,![]() ,
,![]() ,若過頂點
,若過頂點![]() 的一條直線
的一條直線![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,顯然直線
,顯然直線![]() 是
是![]() 的關于點
的關于點![]() 的二分割線.
的二分割線.
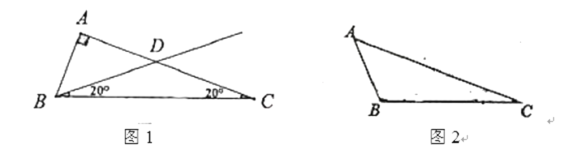
(1)在圖2的![]() 中,
中,![]() ,
,![]() .請在圖2中畫出
.請在圖2中畫出![]() 關于點
關于點![]() 的二分割線,且
的二分割線,且![]() 角度是 ;
角度是 ;
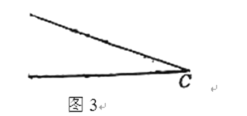
(2)已知![]() ,在圖3中畫出不同于圖1,圖2的
,在圖3中畫出不同于圖1,圖2的![]() ,所畫
,所畫![]() 同時滿足:①
同時滿足:①![]() 為最小角;②存在關于點
為最小角;②存在關于點![]() 的二分割線.
的二分割線.![]() 的度數是 ;
的度數是 ;
(3)已知![]() ,
,![]() 同時滿足:①
同時滿足:①![]() 為最小角;②存在關于點
為最小角;②存在關于點![]() 的二分割線.請求出
的二分割線.請求出![]() 的度數(用
的度數(用![]() 表示).
表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,現將一塊等腰直角三角板ABC放在第二象限,斜靠在兩坐上,且點A(0,2),點C(![]() ,0),如圖所示:拋物線
,0),如圖所示:拋物線![]() 經過點B。
經過點B。
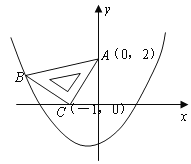
(1)求點B的坐標;
(2)求拋物線的解析式;
(3)在拋物線上是否還存在點P(點B除外),使△ACP仍然是以AC為直角邊的等腰直角三角形?若存在,求所有點P的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
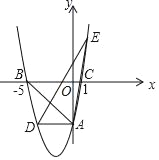
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx﹣5交y軸于點A,交x軸于點B(﹣5,0)和點C(1,0),過點A作AD∥x軸交拋物線于點D.
(1)求此拋物線的表達式;
(2)點E是拋物線上一點,且點E關于x軸的對稱點在直線AD上,求△EAD的面積;
(3)若點P是直線AB下方的拋物線上一動點,當點P運動到某一位置時,△ABP的面積最大,求出此時點P的坐標和△ABP的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,若點
,若點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() ,將線段AE繞著點
,將線段AE繞著點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() .
.
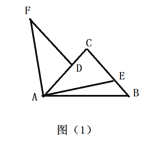
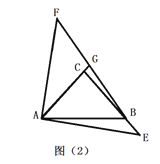
(1)如圖![]() ,當點
,當點![]() 在線段
在線段![]() 上運動時;
上運動時;
①若![]() ,則
,則![]() _______ (直接寫出答案);
_______ (直接寫出答案);
②過![]() 點作
點作![]() 交
交![]() 于
于![]() 點,求證:
點,求證:![]() ;
;
(2)當![]() 點在射線
點在射線![]() 上,(如圖2) 連接
上,(如圖2) 連接![]() 與直線
與直線![]() 交于
交于![]() 點,若
點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
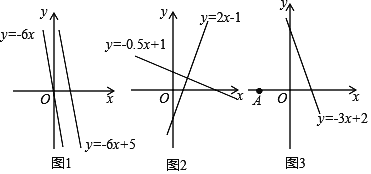
【題目】材料一:如圖1,由課本91頁例2畫函數y=﹣6x與y=﹣6x+5可知,直線y=﹣6x+5可以由直線y=﹣6x向上平移5個單位長度得到由此我們得到正確的結論一:在直線L1:y=K1x+b1與直線L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反過來,也成立.
材料二:如圖2,由課本92頁例3畫函數y=2x﹣1與y=﹣0.5x+1可知,利用所學知識一定能證出這兩條直線是互相垂直的.由此我們得到正確的結論二:在直線L1:y=k1x+b1 與L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反過來,也成立
應用舉例
已知直線y=﹣![]() x+5與直線y=kx+2互相垂直,則﹣
x+5與直線y=kx+2互相垂直,則﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解決問題
(1)請寫出一條直線解析式______,使它與直線y=x﹣3平行.
(2)如圖3,點A坐標為(﹣1,0),點P是直線y=﹣3x+2上一動點,當點P運動到何位置時,線段PA的長度最小?并求出此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有公路l1同側、l2異側的兩個城鎮A,B,如下圖.電信部門要修建一座信號發射塔,按照設計要求,發射塔到兩個城鎮A,B的距離必須相等,到兩條公路l1,l2的距離也必須相等,發射塔C應修建在什么位置?請用尺規作圖找出所有符合條件的點,注明點C的位置.(保留作圖痕跡,不要求寫出畫法)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com