【題目】計算
（1）（﹣3
）﹣（﹣2
）﹣（﹣2
）﹣（+1.75）﹣（﹣1）
（2）﹣4×（﹣2
）﹣6×（﹣2）+17×（﹣2）﹣19
÷
（3）﹣12+
×[﹣22+（﹣3）2×（﹣2）+（﹣3）]÷（﹣
）2
【答案】（1）1；（2）﹣197；（3）﹣
．
【解析】
（1）根據有理數的加減法可以解答本題；
（2）根據有理數的乘除法和加減法可以解答本題；
（3）根據有理數的乘除法和加減法可以解答本題.
（1）（﹣3
）﹣（﹣2
）﹣（﹣2
）﹣（+1.75）﹣（﹣1）
=（﹣3）+2+2+（﹣1）+1
=1；
（2）﹣4×（﹣2
）﹣6×（﹣2）+17×（﹣2）﹣19
÷
=（﹣4﹣6+17）×（﹣2）﹣（19+）×9
=7×（﹣
）﹣19×9﹣8
=（﹣18）﹣171﹣8
=﹣197；
（3）﹣12+
×[﹣22+（﹣3）2×（﹣2）+（﹣3）]÷（﹣
）2
=﹣1+×[-4+(-18)+(-3)] ×
=﹣1+×(-25)×
=﹣1﹣
=﹣．
科目：初中數學 來源： 題型：
【題目】如圖，∠MON=45°，OA1=1，作正方形A1B1C1A2 ， 面積記作S1；再作第二個正方形A2B2C2A3 ， 面積記作S2；繼續(xù)作第三個正方形A3B3C3A4 ， 面積記作S3；點A1、A2、A3、A4…在射線ON上，點B1、B2、B3、B4…在射線OM上，…依此類推，則第6個正方形的面積S6是 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
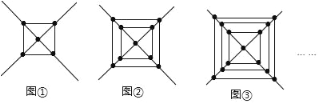
【題目】觀察下列各圖形中點的個數，根據其中蘊含的規(guī)律回答下列問題：
（1）圖①中有 個點；圖②中有 個點；圖③中有 個點；
（2）請用代數式表示出第n個圖形中點個數；并求第10個圖形中共有多少個點？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：點M，N把線段AB分割成AM、MN，NB，若以AM、MN、NB為邊的三角形是一個直角三角形，則稱點M、N是線段AB的勾股分割點．
（1）如圖①，已知M、N是線段AB的勾股分割點，AM=6，MN=8，求NB的長；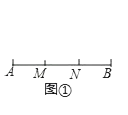
（2）如圖②，在△ABC中，點D、E在邊線段BC上，且BD=3，DE=5，EC=4，直線l∥BC，分別交AB、AD、AE、AC于點F、M、N、G．求證：點M，N是線段FG的勾股分割點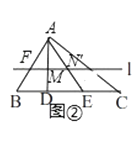
（3）在菱形ABCD中，∠ABC=β（β＜90°），點E、F分別在BC、CD上，AE、AF分別交BD于點M、N．
①如圖③，若BE= 
BC，DF= 
CD，求證：M、N是線段BD的勾股分割點．
②如圖④，若∠EAF= ∠BAD，sinβ= 
，當點M、N是線段AB的勾股分割點時，求BM：MN：ND的值．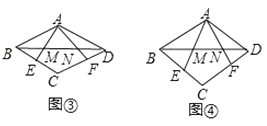
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（題文）如圖，在等腰直角三角形MNC中，CN＝MN＝
，將△MNC繞點C順時針旋轉60°，得到△ABC，連接AM，BM，BM交AC于點O.
(1)∠NCO的度數為________；
(2)求證：△CAM為等邊三角形；
(3)連接AN，求線段AN的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數y＝ax2＋bx＋c(a，b，c是常數，a≠0)圖象的對稱軸是直線x＝1，其圖象的一部分如圖所示，對于下列說法：①abc<0；②當－1<x<3時，y>0；③a－b＋c<0；④3a＋c<0.其中正確的是________(填序號)．
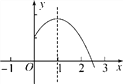
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，點A的坐標為（－2，0），等邊三角形AOC經過平移或軸對稱或旋轉對稱都可以得到△OBD。
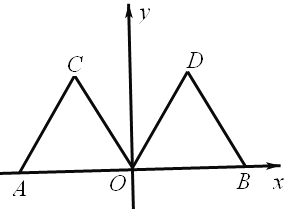
（1）△AOC沿x軸向右平移得到△OBD，則平移的距離是 個單位長度；△AOC與△OBD關于直線對稱，則對稱軸是 ；△AOC繞原點O順時針旋轉得到△OBD，則旋轉角可以是 度；
（2）連接AD，交OC于點E，求∠AEO的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題滿分8分）如圖，四邊形ABCD中，
,E是邊CD的中點，連接BE并延長與AD的延長線相較于點F．
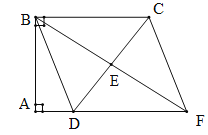
（1）求證：四邊形BDFC是平行四邊形；
（2）若△BCD是等腰三角形，求四邊形BDFC的面積．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com