
【題目】如圖,在矩形ABCD中,AB=3,BC=5,E是AD上的一個(gè)動(dòng)點(diǎn)
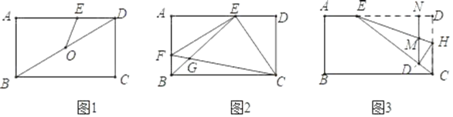
(1)如圖 1,連接 BD,O 是對角線 BD 的中點(diǎn),連接 OE.當(dāng) OE=DE 時(shí),求 AE 的長;
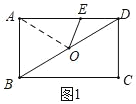
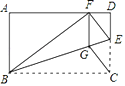
(2)如圖 2,連接 BE,EC,過點(diǎn) E 作 EF⊥EC 交 AB 于點(diǎn) F,連接 CF,與 BE 交于點(diǎn) G.當(dāng)BE 平分∠ABC 時(shí),求 BG 的長;
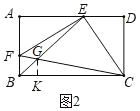
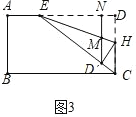
(3)如圖 3,連接 EC,點(diǎn) H 在 CD 上,將矩形 ABCD 沿直線 EH 折疊,折疊后點(diǎn) D 落在 EC上的點(diǎn) D′處,過點(diǎn) D′作 D′N⊥AD 于點(diǎn) N,與 EH 交于點(diǎn) M,且 AE=1.![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求出![]() ,進(jìn)而求出
,進(jìn)而求出![]() ,再判斷
,再判斷![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
(2)先判斷出![]() ,進(jìn)而求出
,進(jìn)而求出![]() ,再判斷出
,再判斷出![]() ,進(jìn)而求得
,進(jìn)而求得![]() ,最后利用勾股定理即可得出結(jié)論;
,最后利用勾股定理即可得出結(jié)論;
(3)先求出![]() ,再求出
,再求出![]() ,根據(jù)勾股定理求出
,根據(jù)勾股定理求出![]() ,
,![]() ,再判斷出
,再判斷出![]() ,
,![]() ,列出比例式,并根據(jù)同高三角形面積的比等于對應(yīng)底邊的比,即可得出結(jié)論;
,列出比例式,并根據(jù)同高三角形面積的比等于對應(yīng)底邊的比,即可得出結(jié)論;
解:(1)如圖 1,連接![]() ,
,
在矩形![]() 中,
中,![]() ,
,
![]() 在
在![]() 中,根據(jù)勾股定理得
中,根據(jù)勾股定理得![]()
∵![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
(2)∵![]() 平分
平分![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如圖 2,過點(diǎn)![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
設(shè)![]() ,則
,則![]()
![]()
解得:![]()
∴![]() ,
,
![]() 在
在![]() 中,
中,![]()
(3)如圖 3,在矩形![]() 中,
中,![]() ,
,
∵![]()
∴![]() ,
,
∵![]() ,
,
∴在![]() 中,由勾股定理可得:
中,由勾股定理可得:![]() ,
,
由折疊知,![]() ,
,
∴![]() ,
,
設(shè)![]() ,則
,則![]()
![]() 在
在![]() 中,根據(jù)勾股定理得,
中,根據(jù)勾股定理得,![]()
解得:![]()
∴![]()
∵![]()
∴![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
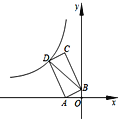
【題目】如圖,點(diǎn)A(-2,0),B(0,1),以線段AB為邊在第二象限作矩形ABCD,雙曲線![]() (k<0)經(jīng)過點(diǎn)D,連接BD,若四邊形OADB的面積為6,則k的值是_____.
(k<0)經(jīng)過點(diǎn)D,連接BD,若四邊形OADB的面積為6,則k的值是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)問題發(fā)現(xiàn)
如圖1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,連接AC,BD交于點(diǎn)M.填空:
①![]() 的值為 ;
的值為 ;
②∠AMB的度數(shù)為 .
(2)類比探究
如圖2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,連接AC交BD的延長線于點(diǎn)M.請判斷![]() 的值及∠AMB的度數(shù),并說明理由;
的值及∠AMB的度數(shù),并說明理由;
(3)拓展延伸
在(2)的條件下,將△OCD繞點(diǎn)O在平面內(nèi)旋轉(zhuǎn),AC,BD所在直線交于點(diǎn)M,若OD=1,OB=![]() ,請直接寫出當(dāng)點(diǎn)C與點(diǎn)M重合時(shí)AC的長.
,請直接寫出當(dāng)點(diǎn)C與點(diǎn)M重合時(shí)AC的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀與思考:
阿基米德(公元前287年一公元前212年),偉大的古希臘哲學(xué)家、百科式科學(xué)家、數(shù)學(xué)家、物理學(xué)家、力學(xué)家,靜態(tài)力學(xué)和流體靜力學(xué)的奠基人,阿基米德流傳于世的著作有10余種,多為希臘文手稿下面是《阿基米德全集》中記載的一個(gè)命題:AB是⊙O的弦,點(diǎn)C在⊙O上,且CD⊥AB于點(diǎn)D,在弦AB上取點(diǎn)E,使AD=DE,點(diǎn)F是![]() 上的一點(diǎn),且
上的一點(diǎn),且![]() =
=![]() ,連接BF可得BF=BE.
,連接BF可得BF=BE.
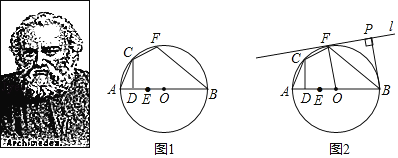
(1)將上述問題中弦AB改為直徑AB,如圖1所示,試證明BF=BE;
(2)如圖2所示,若直徑AB=10,EO=![]() OB,作直線l與⊙O相切于點(diǎn)F.過點(diǎn)B作BP⊥l于點(diǎn)P.求BP的長.
OB,作直線l與⊙O相切于點(diǎn)F.過點(diǎn)B作BP⊥l于點(diǎn)P.求BP的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】新型冠狀病毒爆發(fā),教育部部署了“停課不停學(xué)”的有關(guān)工作,各地都在進(jìn)行在線教育.小依同學(xué)為了了解網(wǎng)課學(xué)習(xí)情況,對本班部分同學(xué)最喜愛的課程進(jìn)行了調(diào)查,調(diào)查課程分別是網(wǎng)上授課、體育鍛煉、名著閱讀、藝術(shù)欣賞和其他課程并制成以下兩幅不完整的統(tǒng)計(jì)圖, 請你根據(jù)圖中提供的信息解答下列問題:
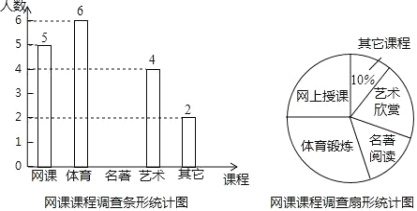
(1)求本次調(diào)查中一共調(diào)查了多少名學(xué)生,及其中“名著閱讀”所占的圓心角度數(shù) .
(2)請把條形統(tǒng)計(jì)圖補(bǔ)全.
(3)若該校一共有 3000 名學(xué)生,請估算出全校最喜愛的課程是“體育鍛煉”的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,下列正方形網(wǎng)格的每個(gè)小正方形的邊長均為1,⊙O的半徑為![]() .規(guī)定:頂點(diǎn)既在圓上又是正方形格點(diǎn)的直角三角形稱為“圓格三角形”,請按下列要求各畫-個(gè)“圓格三角形”.
.規(guī)定:頂點(diǎn)既在圓上又是正方形格點(diǎn)的直角三角形稱為“圓格三角形”,請按下列要求各畫-個(gè)“圓格三角形”.
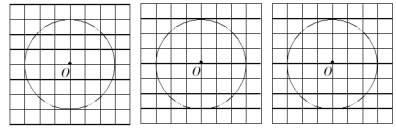
①直角邊長度為整數(shù),②面積為8,③一個(gè)內(nèi)角所對的弧長為![]() π
π
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若二次函數(shù)y=x2﹣2x+2在自變量x滿足m≤x≤m+1時(shí)的最小值為6,則m的值為( )
A. ![]() B.
B. ![]()
C. 1D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD中,點(diǎn)E在邊CD上,將△BCE沿BE折疊,點(diǎn)C落在AD邊上的點(diǎn)F處,過點(diǎn)F作FG∥CD交BE于點(diǎn)G,連接CG.
(1)求證:四邊形CEFG是菱形;
(2)若AB=6,AD=10,求四邊形CEFG的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com