
【題目】已知雙曲線![]() 與直線
與直線![]() 相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線
相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線![]() 上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線
上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線![]() 于點E,交BD于點C.
于點E,交BD于點C.
(1)若點D坐標是(-8,0),求A、B兩點坐標及k的值.
(2)若B是CD的中點,四邊形OBCE的面積為4,求直線CM的解析式.
(3)設直線AM、BM分別與y軸相交于P、Q兩點,且MA=pMP,MB=qMQ,求p-q的值.

【答案】解:(1)∵D(-8,0),∴B點的橫坐標為-8,代入![]() 中,得y=-2.
中,得y=-2.
∴B點坐標為(-8,-2).而A、B兩點關于原點對稱,∴A(8,2).
從而![]() .
.
(2)∵N(0,-n),B是CD的中點,A、B、M、E四點均在雙曲線上,
∴![]() ,B(-2m,-
,B(-2m,-![]() ),C(-2m,-n),E(-m,-n).
),C(-2m,-n),E(-m,-n).
S矩形DCNO![]() ,S△DBO=
,S△DBO=![]() ,S△OEN =
,S△OEN =![]() ,
,
∴S四邊形OBCE= S矩形DCNO-S△DBO- S△OEN=k.∴![]() .
.
由直線![]() 及雙曲線
及雙曲線![]() ,得A(4,1),B(-4,-1),
,得A(4,1),B(-4,-1),
∴C(-4,-2),M(2,2).
設直線CM的解析式是![]() ,由C、M兩點在這條直線上,得
,由C、M兩點在這條直線上,得
![]() 解得
解得![]() .
.
∴直線CM的解析式是![]() .
.
(3)如圖,分別作AA1⊥x軸,MM1⊥x軸,垂足分別為A1、M1.

設A點的橫坐標為a,則B點的橫坐標為-a.于是
![]() .
.
同理![]() ,
,
∴![]() .
.
【解析】(1)根據B點的橫坐標為-8,代入![]() 中,得
中,得![]() ,得出B點的坐標,即可得出A點的坐標,再根據
,得出B點的坐標,即可得出A點的坐標,再根據![]() 求出即可;
求出即可;
分別作![]() ⊥
⊥![]() 軸,
軸,![]() ⊥
⊥![]() 軸,垂足分別為
軸,垂足分別為![]() ,設A點的橫坐標為
,設A點的橫坐標為![]() ,則B點的橫坐標為
,則B點的橫坐標為![]() ,于是
,于是![]() ,同理
,同理![]() ,即可得到結果。
,即可得到結果。


 名題金卷系列答案
名題金卷系列答案科目:初中數學 來源: 題型:
【題目】某校學生數學興趣小組為了解本校同學對上課外補習班的態度,在學校抽取了部分同學進行了問卷調查,調查分別為“A﹣非常贊同”、“B﹣贊同”、“C﹣無所謂”、“D﹣不贊同”等四種態度,現將調查統計結果制成了如圖兩幅統計圖,請結合兩幅統計圖,回答下列問題:
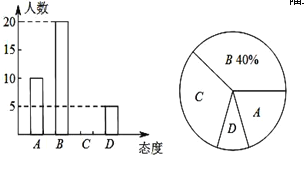
(1)抽取了多少名同學進行了問卷調查?
(2)請補全條形統計圖.
(3)持“不贊同”態度的學生人數的百分比所占扇形的圓心角為 度.
(4)若該校有3000名學生,請你估計該校學生對持“贊同”和“非常贊同”兩種態度的人數之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1) ,折疊平行四邊形![]() ,使得
,使得![]() 分別落在
分別落在![]() 邊上的
邊上的![]() 點,
點,![]() 為折痕
為折痕

(1)若![]() ,證明:平行四邊形
,證明:平行四邊形![]() 是菱形;
是菱形;
(2)若![]() ,求
,求![]() 的大小;
的大小;
(3)如圖(2) ,以![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,若
,若![]() ,求
,求![]() 的大小
的大小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)(觀察思考):
如圖,線段![]() 上有兩個點
上有兩個點![]() ,圖中共有_________條線段;
,圖中共有_________條線段;
![]()
(2)(模型構建):
如果線段上有![]() 個點(包括線段的兩個端點),則該線段上共有___________條線段;
個點(包括線段的兩個端點),則該線段上共有___________條線段;
(3)(拓展應用):
某班8位同學參加班上組織的象棋比賽,比賽采用單循環制(即每兩位同學之間都要進行一場比賽),那么一共要進行__________場比賽.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學課上,王老師出示一道題:解方程![]() .小馬立即舉手并在黑板上寫出了解方程過程,具體如下:
.小馬立即舉手并在黑板上寫出了解方程過程,具體如下:
解:![]() ,
,
去括號,得:![]() .………………①
.………………①
移項,得:![]() .…………………②
.…………………②
合并同類項,得:![]() .……………………③
.……………………③
系數化為1,得:![]() .………………………④
.………………………④
(1)請你寫出小馬解方程過程中哪步錯了,并簡要說明錯誤原因;
(2)請你正確解方程:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上有兩個動點M,N,如果點M始終在點N的左側,我們稱作點M是點N的“追趕點”.如圖,數軸上有2個點A,B,它們表示的數分別為-3,1,已知點M是點N的“追趕點”,且M,N表示的數分別為m,n.
(1)由題意得:點A是點B的“追趕點”,AB=1-(-3)=4(AB表示線段AB的長,以下相同);類似的,MN=____________.
(2)在A,M,N三點中,若其中一個點是另外兩個點所構成線段的中點,請用含m的代數式來表示n.
(3)若AM=BN,MN=![]() BM,求m和n值.
BM,求m和n值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() ,
,![]() 是平面直角坐標系中的任意兩點,我們把
是平面直角坐標系中的任意兩點,我們把![]() 叫做P1,P2兩點間的“直角距離”,記作d(P1,P2);比如:點P(2,-4),Q(1,0),則d(P,Q)=
叫做P1,P2兩點間的“直角距離”,記作d(P1,P2);比如:點P(2,-4),Q(1,0),則d(P,Q)=![]() ,已知Q(2,1),動點P(x,y)滿足d(P,Q)=3,且x,y均為整數,則滿足條件的點P有________個.
,已知Q(2,1),動點P(x,y)滿足d(P,Q)=3,且x,y均為整數,則滿足條件的點P有________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中點,過D分別作DP⊥AF于P,DQ⊥CE于Q,則DP∶DQ等于

A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com