Question

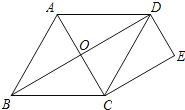
【題目】如圖，BD是邊長為1的正方形ABCD的對角線，BE平分∠DBC交DC于點E，延長BC到點F，使CF=CE，連接DF，交BE的延長線于點G.

（1）求證：△BCE≌△DCF；

（2）求CF的長。

Answer 1

【答案】（1）證明見解析；（2）-1.

【解析】

（1）利用正方形的性質，由全等三角形的判定定理SAS，即可證得△BCE≌△DCF；

（2）由BE平分∠DBC，BD是正方形ABCD的對角線，及△BCE≌△DCF可得∠DEG=∠BEC，∠BGD=∠BCD=90°=∠BGF.從而得到△DBG≌△FBG，根據全等三角形的性質可得BF的長，最后由勾股定理及線段的和差，即可求得CF的長度.

（1）∵四邊形ABCD為正方形，

∴CB=CD，∠BCD=90°，

∴∠DCF=180°-∠BCD=90°，

在△BCE和△DCF中，

，

∴△BCE≌△DCF；

（2）∵BD是正方形ABCD的對角線，

∠DBC=∠ABC==45°，

∵BE平分∠DBC，

∴∠EBC=∠DBC=22.5°，

由（1）知△BCE≌△DCF，

∴∠EBC=∠FDC=22.5°，

∵∠DEG=∠BEC，

∴∠BGD=∠BCD=90°=∠BGF，

在△DBG和△FBG中，

，

∴△DBG≌△FBG，

∴BD=BF，DG=FG，

∵BD=，

∴BF=，

∴CF=BF-BC=-1.