
【題目】如圖,已知二次函數![]() 的圖像與x軸交于A、B兩點(點A在點B左側),與y軸交于點C.
的圖像與x軸交于A、B兩點(點A在點B左側),與y軸交于點C.
(1)求線段BC的長;
(2)當0≤y≤3時,請直接寫出x的范圍;
(3)點P是拋物線上位于第一象限的一個動點,連接CP,當∠BCP=90o時,求點P的坐標.
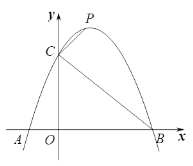
【答案】(1)5 ;(2)![]() ,
,![]() ;(3)點P坐標為(
;(3)點P坐標為(![]() ,
,![]() ).
).
【解析】
(1)分別求出點B和點C的坐標,再運用勾股定理即可求出BC的長;
(2)求出y=0和y=3時相應的x的值,結合函數的圖象即可得到答案;
(3)過點P作PD⊥y軸,設點P坐標為(x, ![]() ),則點D坐標為(0,
),則點D坐標為(0, ![]() ),表示出PD,CD,證明△PDC∽△COB,得出
),表示出PD,CD,證明△PDC∽△COB,得出![]() ,列方程求解即可.
,列方程求解即可.
(1)當x=0時,y=3,
∴C(0,3),
∴OC=3
當y=0時![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
∴A(-1,0),B(4,0),
∴OA=1,OB=4
在Rt△BOC中,BC=![]() =5;
=5;
(2) 當y=0時![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
當y=3時![]() ,解得x1=0,x2=4
,解得x1=0,x2=4
∴當0≤y≤3時,![]() ,
,![]()
(3)過點P作PD⊥y軸

設點P坐標為(x, ![]() ),則點D坐標為(0,
),則點D坐標為(0, ![]() )
)
∴PD=x,CD=![]() -3=
-3=![]()
∵∠BCP=90°,
∴∠PCD+∠BCO=90°,
∵∠PCD+∠CPD=90°,
∴∠BCO=∠CPD
∵∠PDC=∠BOC=90°,
∴△PDC∽△COB
∴![]() ,
,
∴![]() ,
,
∴x=![]() 或x=0(舍去)
或x=0(舍去)
當x=![]() 時,y=
時,y=![]()
∴點P坐標為(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】將矩形![]() 繞點
繞點![]() 順時針旋轉得到矩形
順時針旋轉得到矩形![]() ,點
,點![]() 的對應點分別為
的對應點分別為![]()
(1)當點![]() 落在
落在![]() 上時
上時
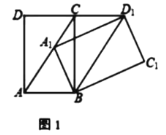
①如圖1,若![]() ,求證:
,求證:![]()
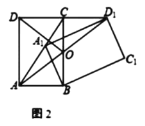
②如圖2,![]() 交
交![]() 于點
于點![]() .若
.若![]() ,求證:
,求證:![]() ;
;
(2)若![]() ,
,
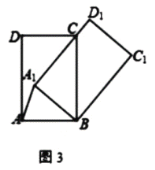
①如圖3,當![]() 過點C時,則
過點C時,則![]() 的長=_____.
的長=_____.
②當![]() 時,作
時,作![]() ,
,![]() 繞點
繞點![]() 轉動,當直線
轉動,當直線![]() 經過
經過![]() 時,直線
時,直線![]() 交邊
交邊![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
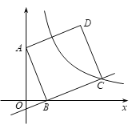
【題目】如圖,在直角坐標系中,正方形ABCD繞點A(0,6)旋轉,當點B落在x軸上時,點C剛好落在反比例函數![]() (k≠0,x>0)的圖像上.已知sin∠OAB=
(k≠0,x>0)的圖像上.已知sin∠OAB=![]() .
.
(1)求反比例函數的表達式;
(2)反比例函數![]() 的圖像是否經過AD邊的中點,并說明理由.
的圖像是否經過AD邊的中點,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
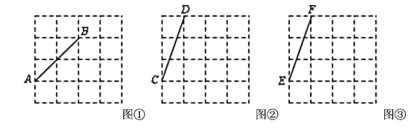
【題目】圖①、圖②、圖③均是4×4的正方形網格,每個小正方形的頂點稱為格點,小正方形的邊長為1,點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格點上,在圖①、圖②、圖③中,只用無刻度的直尺,在給定的網格中按要求畫圖,所畫圖形的頂點均在格點上,不要求長寫出畫法.
均在格點上,在圖①、圖②、圖③中,只用無刻度的直尺,在給定的網格中按要求畫圖,所畫圖形的頂點均在格點上,不要求長寫出畫法.
(1)在圖①中以線段![]() 為邊畫一個直角△
為邊畫一個直角△![]() ;
;
(2)在圖②中以線段![]() 為邊畫一個軸對稱△
為邊畫一個軸對稱△![]() ,使其面積為5;
,使其面積為5;
(3)在圖③中以線段![]() 為邊畫一個軸對稱四邊形
為邊畫一個軸對稱四邊形![]() ,使其面積為6.
,使其面積為6.
查看答案和解析>>
科目:初中數學 來源: 題型:
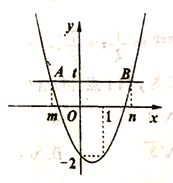
【題目】如圖為二次函數![]() 圖象,直線
圖象,直線![]() 與拋物線交于
與拋物線交于![]() 兩點,
兩點,![]() 兩點橫坐標分別為
兩點橫坐標分別為![]() 根據函數圖象信息有下列結論:
根據函數圖象信息有下列結論:
①![]() ;
;
②若對于![]() 的任意值都有
的任意值都有![]() ,則
,則![]() ;
;
③![]() ;
;
④![]() ;
;
⑤當![]() 為定值時若
為定值時若![]() 變大,則線段
變大,則線段![]() 變長
變長
其中,正確的結論有__________(寫出所有正確結論的番號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司到果園基地購買某種水果慰問醫務工作者,果園基地向購買超過![]() 以上(含
以上(含![]() )的客戶推出兩種購買方式.方式甲:價格為
)的客戶推出兩種購買方式.方式甲:價格為![]() 元
元![]() ,由果園基地運送到公司;方式乙:價格為
,由果園基地運送到公司;方式乙:價格為![]() 元
元![]() ,由顧客自己租車運回,從果園基地到公司的租車費用為
,由顧客自己租車運回,從果園基地到公司的租車費用為![]() 元.設該公司購買水果的數量為
元.設該公司購買水果的數量為![]() (
(![]() ).
).
(1)根據題意,填寫下表:
購買水果的數量(kg) |
|
|
| … |
方式甲的總費用(元) |
| … | ||
方式乙的總費用(元) |
| … |
(2)設該公司按方式甲購買水果的總費用為![]() 元,按方式乙購買水果的總費用為
元,按方式乙購買水果的總費用為![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)根據題意填空:
① 若按方式甲購買水果的總費用和按方式乙購買水果的總費用相同,則該公司購買水果的數量為 ![]() ;
;
② 若該公司購買水果的數量為![]() ,則按方式甲、方式乙中的方式 購買水果的總費用少;
,則按方式甲、方式乙中的方式 購買水果的總費用少;
③ 若該公司購買水果的總費用為![]() 元,則按方式甲、方式乙中的方式 購買水果的數量多.
元,則按方式甲、方式乙中的方式 購買水果的數量多.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]()
![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,已知點
,已知點![]() .
.
(1)若![]() ,求
,求![]() ,
,![]() 滿足的關系式;
滿足的關系式;
(2)直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,拋物線的對稱軸為直線
兩點,拋物線的對稱軸為直線![]() ,且
,且![]() .
.
①求拋物線的解析式(各項系數用含![]() 的式子表示);
的式子表示);
②求線段![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年是脫貧攻堅決勝之年,我市某鄉為了增加農民收入,決定利用當地優質山林土地資源發展園林綠化樹苗培育產業.前期由鄉農技站引進“銀杏”、“羅漢松”、“廣玉蘭”、“竹柏”四個品種共![]() 棵幼苗進行試育成苗實驗,并把實驗數據繪制成下圖所示的扇形統計圖和不完整的條形統計圖,已知實驗中竹柏的成苗率是
棵幼苗進行試育成苗實驗,并把實驗數據繪制成下圖所示的扇形統計圖和不完整的條形統計圖,已知實驗中竹柏的成苗率是![]() .
.
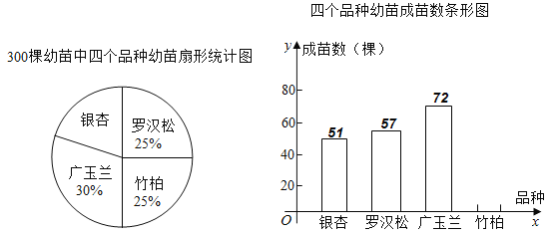
(1)請你補全條形統計圖;
(2)如果從這![]() 棵實驗幼苗中隨機抽取一棵幼苗,求它能成苗的概率;
棵實驗幼苗中隨機抽取一棵幼苗,求它能成苗的概率;
(3)根據市場調查,這四個品種的樹苗的幼苗進價、成苗售價和市場需求如下表所示:
樹苗品種 | 銀杏 | 羅漢松 | 廣玉蘭 | 竹柏 |
每棵幼苗進價(元) |
|
|
|
|
每棵成苗售價(元) |
|
|
|
|
市場需求(萬棵) |
|
|
|
|
假設除了購買幼苗外,培育每棵成苗還需肥料等支出![]() 元(未成功培育成成苗的此項支出忽略不計),該鄉根據市場需求組織
元(未成功培育成成苗的此項支出忽略不計),該鄉根據市場需求組織![]() 村農民培育銀杏樹苗和羅漢松樹苗并將全部成苗銷售完成后,可為本鄉
村農民培育銀杏樹苗和羅漢松樹苗并將全部成苗銷售完成后,可為本鄉![]() 村農民增加收入多少萬元?
村農民增加收入多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月23日為世界閱讀日,為響應黨中央“倡導全民閱讀,建設書香社會”的號召,某校團委組織了一次全校學生參加的“讀書活動”大賽,為了了解本次大賽的成績,校團委隨機抽取了部分學生的成績(成績![]() 取整數,總分100分)作為樣本進行統計,繪制了如下不完整的頻數頻率分布表和頻數分布直方圖:
取整數,總分100分)作為樣本進行統計,繪制了如下不完整的頻數頻率分布表和頻數分布直方圖:
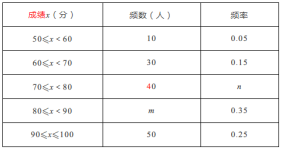
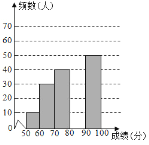
根據所給信息,解答下列問題
(1)抽取的樣本容量是 .![]() .
.![]() .
.
(2)補全頻數分布直方圖,這200名學生成績的中位數會落在 分數段;
(3)全校有1200名學生參加比賽,若得分為90分及以上為優秀,請你估計全校參加比賽成績優秀的學生人數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com