
【題目】如圖,在正方形ABCD中,點C1在邊BC上,將△C1CD繞點D順時針旋轉90°得到△A1AD.A1F平分∠BA1C1,交BD于點F,過點F作FE⊥A1C1,垂足為E,當A1E=3,C1E=2時,則BD的長為_____.

【答案】![]()
【解析】
連接C1F,作FH⊥AB于H,FG⊥BC于G,如圖,

∵四邊形ABCD為正方形,
∴FB平分∠HBG,
而A1F平分∠BA1C1,
∴C1F平分∠GC1E,
∴FH=FG=FE,
易得△A1HF≌△A1EF,△C1GF≌△C1EF,四邊形BGFH為正方形,
∴A1H=A1E=3,C1G=C1E=2,
設BG=BH=x,
在Rt△A1BC1中,(2+x)+(3+x)=52,解得x1=1,x2=6(舍去),
∴A1B=4,BC1=3,
∵△C1CD繞點D順時針旋轉90得到△A1AD,
∴A1A=C1C,
而AB=BC,
∴4CC1=3+C1C,解得C1C=![]() ,
,
∴BC=3+![]() =
=![]() ,
,
∴BD=![]() BC=.
BC=.
故答案為![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=-![]() x+
x+![]() 分別與x軸、y軸交于B、C兩點,點A在x軸上,∠ACB=90°,拋物線
分別與x軸、y軸交于B、C兩點,點A在x軸上,∠ACB=90°,拋物線![]() =ax2+bx+
=ax2+bx+![]() 經過A、B兩點.
經過A、B兩點.
(1)求A、B兩點的坐標;
(2)求拋物線的解析式;
(3)點M是直線BC上方拋物線上的一點,過點M從作MH⊥BC于點H,作軸MD∥y軸交BC于點D,求![]() DMH周長的最大值.
DMH周長的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某高樓OB上有一旗桿CB,我校數學興趣小組的同學準備利用所學的三角函數知識估測該高樓的高度,由于有其他建筑物遮擋視線不便測量,所以測量員沿坡度i=1:![]() 的山坡從坡腳的A處前行50米到達P處,測得旗桿頂部C的仰角為45°,旗桿底部B的仰角為37°(測量員的身高忽略不計),已知旗桿高BC=15米,則該高樓OB的高度為( )米.(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
的山坡從坡腳的A處前行50米到達P處,測得旗桿頂部C的仰角為45°,旗桿底部B的仰角為37°(測量員的身高忽略不計),已知旗桿高BC=15米,則該高樓OB的高度為( )米.(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. 45 B. 60 C. 70 D. 85
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個正整數,由N個數字組成,若它的第一位數可以被1整除,它的前兩位數可以被2整除,前三位數可以被3整除,…,一直到前N位數可以被N整除,則這樣的數叫做“精巧數”.如:123的第一位數“1”可以被1整除,前兩位數“12”可以被2整除,“123”可以被3整除,則123是一個“精巧數”.
(1)若四位數![]() 是一個“精巧數”,求k的值;
是一個“精巧數”,求k的值;
(2)若一個三位“精巧數”![]() 各位數字之和為一個完全平方數,請求出所有滿足條件的三位“精巧數”.
各位數字之和為一個完全平方數,請求出所有滿足條件的三位“精巧數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠OEC的度數是( )

A.128°B.118°C.108°D.98°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD的邊長為3,∠BAD=60°.
(1)連接AC,過點D作DE⊥AB于點E,DF⊥BC交AC于點F,DE、DF于點M、N.
①依題意補全圖1;
②求MN的長;
(2)如圖2,將(1)中∠EDF以點D為中心,順時針旋轉45°,其兩邊DE′、DF′分別與直線AB、BC相交于點Q、P,連接QP,請寫出求△DPQ的面積的思路.(可以不寫出計算結果)

查看答案和解析>>
科目:初中數學 來源: 題型:
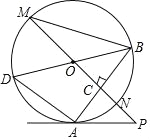
【題目】如圖,已知⊙O中,AB為弦,直線PO交⊙O于點M、N,PO⊥AB于C,過點B作直徑BD,連接AD、BM、AP.
(1)求證:PM∥AD;
(2)若∠BAP=2∠M,求證:PA是⊙O的切線;
(3)若AD=6,tan∠M=![]() ,求⊙O的直徑.
,求⊙O的直徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com