
【題目】某數學興趣小組的同學在研究函數![]() 的圖象時,先對函數
的圖象時,先對函數![]() 的圖象進行了如下探索.
的圖象進行了如下探索.
![]() ①列表:列出
①列表:列出![]() 與
與![]() 的幾組對應值如下:
的幾組對應值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描點:根據表中數據描點如圖所示;
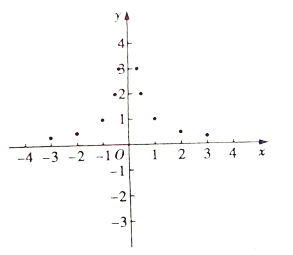
③連線:請在圖中畫出函數![]() 的圖象;
的圖象;
④觀察圖象,寫出兩條關于該函數的性質.
![]() 根據以上探究結果,完成下列問題:
根據以上探究結果,完成下列問題:
①函數![]() 中,自變量
中,自變量![]() 的取值范圍為 ;
的取值范圍為 ;
②函數![]() 的圖象可由函數
的圖象可由函數![]() 的圖象經過怎樣的變換得到?
的圖象經過怎樣的變換得到?
③寫出兩條關于函數![]() 的性質;
的性質;
④直接寫出不等式![]() 的解集.
的解集.
【答案】(1)③見解析;④該函數圖象關于![]() 軸對稱;當
軸對稱;當![]() 時,
時,![]() 隨
隨![]() 增大而減小,當
增大而減小,當![]() 時,
時,![]() 隨
隨![]() 增大而增大;(2)①
增大而增大;(2)①![]() ;②函數
;②函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,可得到函數
個單位長度,可得到函數![]() 的圖象;③圖象
的圖象;③圖象![]() 關于直線對稱;圖象在直線
關于直線對稱;圖象在直線![]() 上側;④
上側;④![]() 或
或![]()
【解析】
(1)③根據描出的點畫圖即可;
④根據圖像寫出性質即可;
(2) ①根據分母不能為0寫出取值范圍即可;②根據研究結果,即可得到變換;③函數![]() 的性質類推寫出即可;④結合圖像和性質直接寫出來即可;
的性質類推寫出即可;④結合圖像和性質直接寫出來即可;
(1) ③圖如下所示:
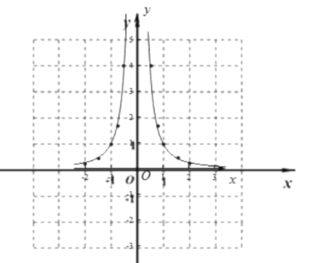
④ 根據函數圖像可知以下性質:a.該函數圖象關于![]() 軸對稱;
軸對稱;
b.當![]() 時,
時,![]() 隨
隨![]() 增大而減小,當
增大而減小,當![]() 時,
時,![]() 隨
隨![]() 增大而增大;
增大而增大;
c.該函數圖象在![]() 軸上方.(答案不唯一,答對兩條即可)
軸上方.(答案不唯一,答對兩條即可)
(2) ①∵函數![]() ,
,
∴![]() ,
,
∴![]() (分母不能為0);
(分母不能為0);
②函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,可得到函數
個單位長度,可得到函數![]() 的圖象.
的圖象.
③a.圖象關于直線![]() 對稱;
對稱;
b.當![]() 時,
時,![]() 隨x增大而減小,當
隨x增大而減小,當![]() 時,
時,![]() 隨
隨![]() 增大而增大;
增大而增大;
e.圖象在直線![]() 上側.(答案不唯一,答對兩條即可)
上側.(答案不唯一,答對兩條即可)
④根據下面函數圖像,直接寫出解集為:![]() 或
或![]() ,
,
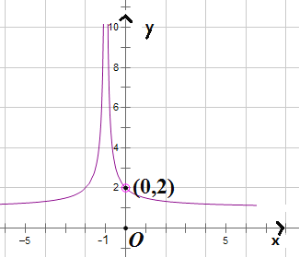


科目:初中數學 來源: 題型:
【題目】春節期間,某商場計劃購進甲、乙兩種商品,已知購進甲商品2件和乙商品3件共需270元;購進甲商品3件和乙商品2件共需230元.
(1)求甲、乙兩種商品每件的進價分別是多少元?
(2)商場決定甲商品以每件40元出售,乙商品以每件90元出售,為滿足市場需求,需購進甲、乙兩種商品共100件,且甲種商品的數量不少于乙種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
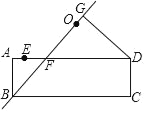
【題目】如圖,矩形ABCD中,AB=3,AD=9,點E在邊AD上,AE=1,過E、D兩點的圓的圓心O在邊AD的上方,直線BO交AD于點F,作DG⊥BO,垂足為G.當△ABF與△DFG全等時,⊙O的半徑為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,AB為⊙O的直徑,弦CD⊥AB于點E,在CD的延長線上取一點P,PG與⊙O相切于點G,連接AG交CD于點F.
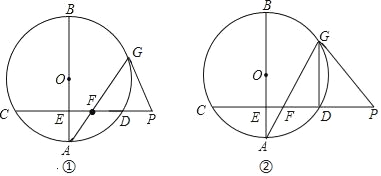
(Ⅰ)如圖①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如圖②,若E為半徑OA的中點,DG∥AB,且OA=2![]() ,求PF的長.
,求PF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與x軸分別交于
與x軸分別交于![]() ,
,![]() 兩點,與y軸交于點C.
兩點,與y軸交于點C.
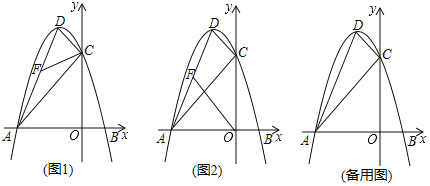
(1)求拋物線的表達式及頂點D的坐標;
(2)點F是線段AD上一個動點.
①如圖1,設![]() ,當k為何值時,
,當k為何值時,![]() .
.
②如圖2,以A,F,O為頂點的三角形是否與![]() 相似?若相似,求出點F的坐標;若不相似,請說明理由.
相似?若相似,求出點F的坐標;若不相似,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩座倉庫分別有農用車12輛和6輛.現在需要調往A縣10輛,需要調往B縣8輛,已知從甲倉庫調運一輛農用車到A縣和B縣的運費分別為40元和80元;從乙倉庫調運一輛農用車到A縣和B縣的運費分別為30元和50元.
(1)設乙倉庫調往A縣農用車x輛,先填好下表,再寫出總運費y關于x的函數關系式;

(2)若要求總運費不超過900元,問共有幾種調運方案?
(3)求出總運費最低的調運方案,最低運費是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com