【題目】如圖，在△ABC中，∠ACB=90°，AC=4，BC=2．P是AB邊上一動點，PD⊥AC于點D，點E在P的右側，且PE=1，連結CE．P從點A出發，沿AB方向運動，當E到達點B時，P停止運動．在整個運動過程中，圖中陰影部分面積S1+S2的大小變化情況是（ ）
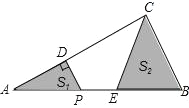
A. 一直減小B. 一直不變C. 先減小后增大D. 先增大后減小
科目：初中數學 來源： 題型：
【題目】如圖，BD為△ABC外接圓⊙O的直徑，且∠BAE=∠C．
（1）求證：AE與⊙O相切于點A；
（2）若AE∥BC，BC=2
，AC=2
，求AD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，一次函數y=－2x與二次函數y＝ax2＋2ax＋c的圖像交于A、B兩點(點A在點B的右側)，與其對稱軸交于點C．
（1）求點C的坐標；
（2）設二次函數圖像的頂點為D，點C與點D關于 x軸對稱，且△ACD的面積等于2.
① 求二次函數的解析式；
② 在該二次函數圖像的對稱軸上求一點P（寫出其坐標），使△PBC與△ACD相似.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知四邊形ABCD內接于圓O，連結BD，∠BAD=105°，∠DBC=75°．
（1）求證：BD=CD；
（2）若圓O的半徑為3，求
的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：Rt△ABC 中，AC＝BC，∠ACB＝90°，D 為 BC 邊中點，CF⊥AD 交 AD 于 E，交 AB 于 F，BE交 AC 于 G，連 DF，下列結論：①AC＝AF，②CD＋DF＝AD，③∠ADC＝∠BDF，④CE＝BE，⑤∠ BED＝45°，其中正確的有（ ）
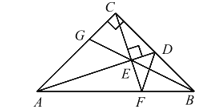
A. 5 個B. 4 個C. 3 個D. 2 個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點 P 是∠AOB 內部一定點
（1）若∠AOB＝50°，作點 P 關于 OA 的對稱點 P1，作點 P 關于 OB 的對稱點 P2，連 OP1、OP2，則∠P1OP2＝___.
（2）若∠AOB＝α，點 C、D 分別在射線 OA、OB 上移動，當△PCD 的周長最小時，則∠CPD＝___（用 α 的代數式表示）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐：某“綜合與實踐”小組開展了“正方體紙盒的制作”實踐活動，他們利用長為
，寬為
長方形紙板制作出兩種不同方案的正方體盒子， 請你動手操作驗證并完成任務．(紙板厚度及接縫處忽略不計)
動手操作一：
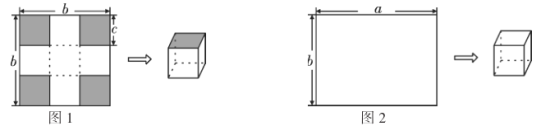
如圖1，若
，按如圖1所示的方式先在紙板四角剪去四個同樣大小邊長為
的小正方形，再沿虛線折合起來就可以做成一個無蓋的正方體紙盒．
問題解決：（1）此時，你發現
與
之間存在的數量關系為 ．
動手操作二：
如圖2，若
，現在在紙板的四角剪去兩個小正方形和兩個小長方形恰好可以制作成一個有蓋的正方體紙盒，其大小與（1）中無蓋正方體大小一樣．
拓展延伸：（2）請你在圖2中畫出你剪去的兩個小正方形和兩個小長方形(用陰影表示)，折痕用虛線表示；
（3）此時，你發現
與之間存在的數量關系為 ；若
，求有蓋正方體紙盒的表面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面的證明
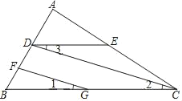
（1）如圖，FG∥CD，∠1＝∠3，∠B＝50°，求∠BDE的度數．
解：∵FG∥CD（已知）
∴∠2＝
又∵∠1＝∠3，
∴∠3＝∠2（等量代換）
∴BC∥
∴∠B+ ＝180°
又∵∠B＝50°
∴∠BDE＝ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了了解九年級學生（共450人）的身體素質情況，體育老師對九（1）班的50位學生進行一分鐘跳繩次數測試，以測試數據為樣本，繪制了如下部分頻數分布表和部分頻數分布直方圖．
組別 | 次數x | 頻數（人數） |
A | 80≤x＜100 | 6 |
B | 100≤x＜120 | 8 |
C | 120≤x＜140 | m |
D | 140≤x＜160 | 18 |
E | 160≤x＜180 | 6 |
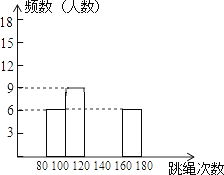
請結合圖表解答下列問題：
（1）表中的m=________；
（2）請把頻數分布直方圖補完整；
（3）這個樣本數據的中位數落在第________組；
（4）若九年級學生一分鐘跳繩次數（x）合格要求是x≥120，則估計九年級學生中一分鐘跳繩成績不合格的人數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
