
【題目】如圖,在△OAB中,頂點O(0,0),A(﹣2,3),B(2,3),將△OAB與正方形ABCD組成的圖形繞點O順時針旋轉,每次旋轉90°,則第2020次旋轉結束時,點D的坐標為( )
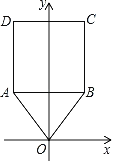
A.(﹣2,7)B.(7,2)C.(2,﹣7)D.(﹣7,﹣2)
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,點E、F分別在邊AB和CD上,下列條件不能判定四邊形DEBF一定是平行四邊形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系![]() 中,半徑為1的
中,半徑為1的![]() 與
與![]() 軸正半軸和
軸正半軸和![]() 軸正半軸分別交于
軸正半軸分別交于![]() 兩點,直線
兩點,直線![]() :
:![]() 與
與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 兩點.
兩點.

(l)當直線![]() 與
與![]() 相切時,求出點
相切時,求出點![]() 的坐標和點
的坐標和點![]() 的坐標;
的坐標;
(2)如圖2,當點![]() 在線段
在線段![]() 上時,直線
上時,直線![]() 與
與![]() 交于
交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的上方),過點
的上方),過點![]() 作
作![]() 軸,與
軸,與![]() 交于另一點
交于另一點![]() ,連結
,連結![]() 交
交![]() 軸于點
軸于點![]() .
.
①如圖3,若點![]() 與點
與點![]() 重合時,求
重合時,求![]() 的長并寫出解答過程;
的長并寫出解答過程;
②如圖2,若點![]() 與點
與點![]() 不重合時,
不重合時,![]() 的長是否發生變化,若不發生變化,請求出
的長是否發生變化,若不發生變化,請求出![]() 的長并寫出解答過程;若發生變化,請說明理由.
的長并寫出解答過程;若發生變化,請說明理由.
(3)如圖4,在(2)的基礎上,連結![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 到
到![]() ,若點
,若點![]() 在
在![]() 的延長線時,請用等式直接表示線段
的延長線時,請用等式直接表示線段![]() ,
,![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
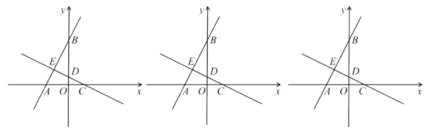
【題目】已知:如圖,在平面直角坐標系中,點![]() 為坐標原點,
為坐標原點,![]() .直線
.直線![]() 與
與![]() 軸交于點A,交
軸交于點A,交![]() 軸于點B.過C點作直線AB的垂線,垂足為E,交
軸于點B.過C點作直線AB的垂線,垂足為E,交![]() 軸于點D.
軸于點D.
(1)求直線CD的解析式;
(2)點G為![]() 軸負半軸上一點,連接EG,過點E作
軸負半軸上一點,連接EG,過點E作![]() 交
交![]() 軸于點H.設點G的坐標為
軸于點H.設點G的坐標為![]() ,線段AH的長為
,線段AH的長為![]() .求
.求![]() 與
與![]() 之間的函數關系式(不要求寫出自變量的取值范圍)
之間的函數關系式(不要求寫出自變量的取值范圍)
(3)過點C作![]() 軸的垂線,過點G作
軸的垂線,過點G作![]() 軸的垂線,兩線交于點M,過點H作
軸的垂線,兩線交于點M,過點H作![]() 于點N,交直線CD于點
于點N,交直線CD于點![]() ,連接MK,若MK平分
,連接MK,若MK平分![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
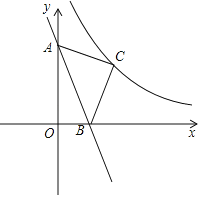
【題目】如圖,在平面直角坐標系中,將直線y=﹣3x向上平移3個單位,與y軸、x軸分別交于點A、B,以線段AB為斜邊在第一象限內作等腰直角三角形ABC.若反比例函數y=![]() (x>0)的圖象經過點C,求此反比例函數的表達式.
(x>0)的圖象經過點C,求此反比例函數的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
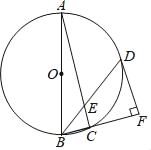
【題目】如圖,△ABC是⊙O的內接圓,且AB是⊙O的直徑,點D在⊙O上,BD平分∠ABC交AC于點E,DF⊥BC交BC延長線于點F.
(1)求證:DF是⊙O的切線.
(2)若![]() ,求DE的長.
,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一塊含30°(即∠CAB=30°)角的三角板和一個量角器拼在一起,三角板斜邊AB與量角器所在圓的直徑MN恰好重合,其量角器最外緣的讀數是從N點開始(即N點的讀數為0°),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E.
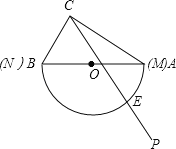
(1)當旋轉7.5秒時,連接BE,試說明:BE=CE;
(2)填空:①當射線CP經過△ABC的外心時,點E處的讀數是 .
②當射線CP經過△ABC的內心時,點E處的讀數是 ;
③設旋轉x秒后,E點出的讀數為y度,則y與x的函數式是y= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
背景閱讀:旋轉就是將圖形上的每一點在平面內繞著旋轉中心旋轉固定角度的位置移動,其中“旋”是過程,“轉”是結果.旋轉作為圖形變換的一種,具備圖形旋轉前后對應點到旋轉中心的距離相等:對應點與旋轉中心所連線段的夾角等于旋轉角:旋轉前、后的圖形是全等圖形等性質.所以充分運用這些性質是在解決有關旋轉問題的關健.
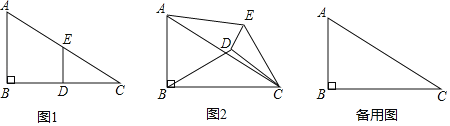
實踐操作:如圖1,在Rt△ABC中,∠B=90°,BC=2AB=12,點D,E分別是邊BC,AC的中點,連接DE,將△EDC繞點C按順時針方向旋轉,記旋轉角為α.
問題解決:(1)①當α=0°時,![]() = ;②當α=180°時,
= ;②當α=180°時,![]() = .
= .
(2)試判斷:當0°≤a<360°時,![]() 的大小有無變化?請僅就圖2的情形給出證明.
的大小有無變化?請僅就圖2的情形給出證明.
問題再探:(3)當△EDC旋轉至A,D,E三點共線時,求得線段BD的長為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com