
【題目】在四邊形ABCD中,AB=AD,BC=CD.
(1)如圖1,請連接AC,BD,求證:AC垂直平分BD;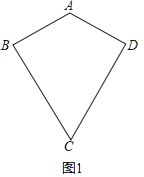
(2)如圖2,若∠BCD=60°,∠ABC=90°,E,F分別為邊BC,CD上的動點,且∠EAF=60°,AE,AF分別與BD交于G,H,求證:△AGH∽△AFE;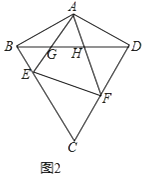
(3)如圖3,在(2)的條件下,若 EF⊥CD,直接寫出 ![]() 的值.
的值.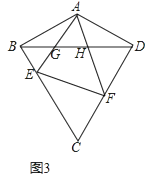
【答案】
(1)解:證明:如圖1中,連接BD、AC.
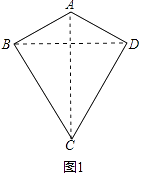
∵AB=AD,
∴點A在線段BD的垂直平分線上,
∵CB=CD,
∴點C在線段BD的垂直平分線上,
∴AC是線段BD的垂直平分線,
即AC垂直平分線段BD.
(2)解:如圖2中,將△ABE繞點A逆時針旋轉120得到△ADM.連接AC交BD于O.
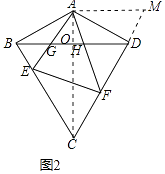
∵B、D關于AC對稱,
∴∠ABC=∠ADC=90°,
∵∠BCD=60°,
∴∠BAD=120°,
∵∠EAF=60°,
∴∠BAE+∠DAF=∠DAF+∠DAM=60°,
∴∠FAE=∠FAM,
∵∠ADM=∠ABE=90°=∠ADF,
∴F、D、M共線,
∵FA=FA,AE=AM,
∴△FAE≌△FAM,
∴∠AFE=∠AFM,
∵∠CAD=∠CAB=60°=∠EAF,
∴∠GAO=∠DAF,
∵∠AGO+∠GAO=90°,∠AFD+∠FAD=90°,
∴∠AGO=∠ADF,
∴∠AGH=∠AFE,∵∠GAH=∠FAE,
∴△AGH∽△AFE.
(3)解:如圖3中,連接AC交BD于O,作HM⊥AD于M.
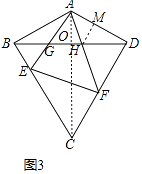
∵EF⊥CD,
∴∠EFD=90°,
由(2)可知∠AFD=∠AFE=∠AGO=45°,
∵∠ADF=90°,
∴AD=DF,設HM=AM=a,則DH=2a,DM= ![]() a,
a,
在Rt△ACD中,∵∠ACD=30°,AD=(1+ ![]() )a,
)a,
∴CD=BD= ![]() AD=(3+
AD=(3+ ![]() )a,
)a,
在Rt△AHD中,∵∠ADH=30°,AD=(1+ ![]() )a,
)a,
∴AO=OG= ![]() AD=
AD= ![]() a,OD=
a,OD= ![]() OA=
OA= ![]() a,
a,
∴OH=OD﹣DH= ![]() a﹣2a=
a﹣2a= ![]() a,
a,
∴GH=OG+OH= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)利用垂直平分線的判定定理及兩點確定一條直線可證出;(2)通過旋轉構造全等三角形,即△FAE≌△FAM,進而得出∠AFE=∠AFM,∠GAH=∠FAE,證出相似;(3)利用(2)的結論得出∠ADF=90°,AD=DF,設出參數HM=AM=a,運用三角函數定義,用a的代數式分別表示出BD,GH,可求出比值.
【考點精析】本題主要考查了相似三角形的判定與性質和銳角三角函數的定義的相關知識點,需要掌握相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方;銳角A的正弦、余弦、正切、余切都叫做∠A的銳角三角函數才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
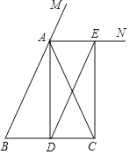
【題目】已知:如圖,在△ABC中,AB=AC,AD是△ABC的中線,AN為△ABC的外角∠CAM的平分線,CE∥AD,交AN于點E.求證:四邊形ADCE是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新定義:我們把只有一組對角是直角的四邊形叫做準矩形.
(1)圖①、圖②均為3×3的正方形網格,每個小正方形的頂點稱為格點,每個小正方形的邊長均為1.線段AB、BC的端點均在格點上,在圖①、圖②中各畫一個準矩形ABCD,要求:準矩形ABCD的頂點D在格點上,且兩個準矩形不全等.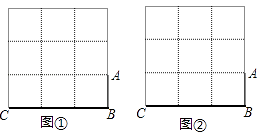
(2)如圖③,正方形ABCD的邊長為4,準矩形ABMN的頂點M、N分別在正方形ABCD的邊上.若準矩形ABMN的一條對角線長為5,直接寫出此時該準矩形的面積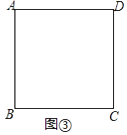
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)和正比例函數y= ![]() x的圖象如圖所示,則方程ax2+(b﹣
x的圖象如圖所示,則方程ax2+(b﹣ ![]() )x+c=0(a≠0)的兩根之和( )
)x+c=0(a≠0)的兩根之和( )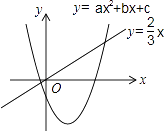
A.大于0
B.等于0
C.小于0
D.不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠計劃生產A、B兩種產品共10件,其生產成本和利潤如下表.
A種產品 | B種產品 | |
成本(萬元/件) | 2 | 5 |
利潤(萬元/件) | 1 | 3 |
(1)若工廠計劃獲利14萬元,問A,B兩種產品應分別生產多少件?
(2)若工廠計劃投入資金不多于44萬元,且獲利多于14萬元,求工廠的最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過半徑為6的圓O上一點A作圓O的切線l,P為圓O的一個動點,作PH⊥l于點H,連接PA.如果PA=x,AH=y,那么下列圖象中,能大致表示y與x的函數關系的是( )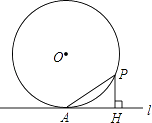
A.
B.
C.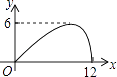
D.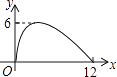
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲、乙兩名射擊選手中選出一名選手參加省級比賽,現對他們分別進行5次射擊測試,成績分別為(單位:環)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲運動員5次射擊成績的中位數為________環,極差是________環;乙運動員射擊成績的眾數為________環.
(2)已知甲的5次成績的方差為2,通過計算,判斷甲、乙兩名運動員誰的成績更穩定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組 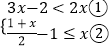 請結合題意填空,完成本題的解答.
請結合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
(Ⅳ)原不等式組的解集為 . ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com