
【題目】如圖,一次函數的圖象過![]() 兩點.
兩點.

(1)求直線![]() 的函數表達式
的函數表達式
(2)直線![]() 交
交![]() 軸于點
軸于點![]() 為直線
為直線![]() 上一動點
上一動點
①求![]() 的最小值;
的最小值;
②![]() 是直線
是直線![]() 上任意一點,
上任意一點,![]() 為直線
為直線![]() 上另一動點,若
上另一動點,若![]() 是以
是以![]() 為直角邊長的等腰直角三角形,求
為直角邊長的等腰直角三角形,求![]() 點的坐標.
點的坐標.
【答案】(1)y=-x+3 (2)① ![]() ② D(-1,0) D(
② D(-1,0) D(![]() ,
,![]() )
)
【解析】
(1)代入A,B點的坐標,即可求出解析式;
(2)①由點到直線距離最短為垂線段,根據△ACE為等腰直角三角形求出CE即可
②分類討論:當DE為斜邊時,D點和C重合,根據上問直接寫出即可;
當DF為斜邊時,D點和C重合,根據上問直接寫出即可;
當EF為斜邊時,作出△DEF,GN⊥x軸 ED延長線交GN于M,通過△EGD∽△AGC,求出GE的值,根據勾股定理求出GM,即可求出D的縱坐標,代入解析式![]() 得到D的坐標
得到D的坐標
解:(1)設直線![]() 的函數表達式為 y=kx+b
的函數表達式為 y=kx+b
將![]() 代入
代入
得![]() 解得
解得![]()
直線![]() 的函數表達式為 y=-x+3
的函數表達式為 y=-x+3
(2)①如圖

作CE⊥AB于E
∵直線![]() 交
交![]() 軸于點C
軸于點C
∴ C(-1,0)
∵![]()
∴△AOB為等腰直角三角形,∠BAO=45°
∴△CEA為等腰直角三角形
∵AC=4
∴CE=![]()
② 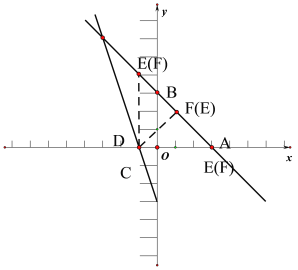
如上圖當以DE為斜邊時,DF=![]()
∵ CE=![]()
∴ C與D重合
∴D(-1,0)
如上圖當以DF為斜邊時,DE=![]() 同理
同理
得到D(-1,0)
如圖 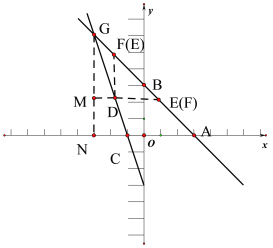
當以EF為斜邊時,DE=DF=![]() ∠DEF=∠DFE=45°
∠DEF=∠DFE=45°
根據題意兩直線解析式可以求出G(-3,6) 如上圖作出△DEF,GN⊥x軸 ED延長線交GN于M 得到GN=6 AG= ∵∠DEF=45° ∠CAB=45° ∴DE∥AC ∵∠AGC是△EGD和△AGC的公共角 ∴△EGD∽△AGC ∴ 解得GE=6 ∵∠DEF=45° ∴GM= ∴MN= ∴D 點的縱坐標為 代入 ∴D( 故答案為:(1)y=-x+3 (2)① ![]()
![]()
![]()
![]()
![]()
![]() 中,解得x=
中,解得x=![]()
![]() ,
,![]() )
)![]() ② D(-1,0) D(
② D(-1,0) D(![]() ,
,![]() )
)


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,AB=AC,AD平分∠BAC交BC于點D,在線段AD上任取一點P(點A除外),過點P作EF∥AB.分別交AC、BC于點E和點F,作PQ∥AC,交AB于點Q,連接QE.
中,AB=AC,AD平分∠BAC交BC于點D,在線段AD上任取一點P(點A除外),過點P作EF∥AB.分別交AC、BC于點E和點F,作PQ∥AC,交AB于點Q,連接QE.
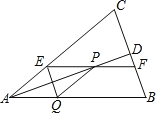
(1)求證:四邊形AEPQ為菱形:
(2)當點P在線段EF上的什么位置時,菱形AEPQ的面積為四邊形EFBQ面積的一半?請說明理
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AE⊥BC于點E,延長BC至點F使CF=BE,連結AF,DE,DF.
(1)求證:四邊形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的長.
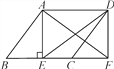
查看答案和解析>>
科目:初中數學 來源: 題型:
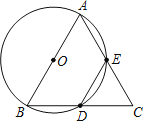
【題目】如圖,在△ABC中,AB=BC=2,以AB為直徑的⊙O分別交BC、AC于點D、E,且點D為BC的中點.
(1)求證:△ABC為等邊三角形;
(2)求DE的長;
(3)在線段AB的延長線上是否存在一點P,使△PBD≌△AED?若存在,請求出PB的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分9分)如圖,點O為Rt△ABC斜邊AB上的一點,以OA為半徑的⊙O與BC切于點D,與AC交于點E,連接AD.

(1)求證:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求陰影部分的面積(結果保留![]() ).
).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:在平面直角坐標系中,對于任意兩點![]() ,
,![]() ,若點
,若點![]() 滿足
滿足![]() ,
,![]() 那么稱點
那么稱點![]() 是點
是點![]() ,
,![]() 的融合點,例如:
的融合點,例如:![]() ,
,![]() ,當點
,當點![]() 滿足
滿足![]() ,
,![]() 時,則點
時,則點![]() 是點
是點![]() ,
,![]() 的融合點.
的融合點.
(1)已知點![]() ,
,![]() ,
,![]() ,請說明其中一個點是另外兩個點的融合點.
,請說明其中一個點是另外兩個點的融合點.
(2)如圖,點![]() ,點
,點![]() 是直線
是直線![]() 上任意一點,點
上任意一點,點![]() 是點
是點![]() ,
,![]() 的融合點.
的融合點.

①試確定![]() 與
與![]() 的關系式;
的關系式;
②在給定的坐標系![]() 中,畫出①中的函數圖象;
中,畫出①中的函數圖象;
③若直線![]() 交
交![]() 軸于點
軸于點![]() .當
.當![]() 為直角三角形時,直接寫出點
為直角三角形時,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com