
【題目】在平面直角坐標系xOy 中,點A 的坐標為(1,0),P 是第一象限內任意一點,連接PO,PA,若∠POA=m°,∠PAO=n°,則我們把(m°,n°)叫做點P 的“雙角坐標”.例如,點(1,1)的“雙角坐標”為(45°,90°).若點P到x軸的距離為![]() ,則m+n 的最小值為___.
,則m+n 的最小值為___.
 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
【題目】某商場統計了每個營業員在某月的銷售額,繪制了如下的條形統計圖以及不完整的扇形統計圖:
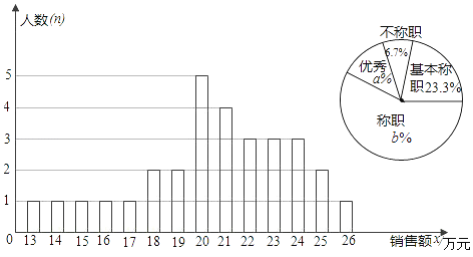
解答下列問題:
(1)設營業員的月銷售額為x(單位:萬元),商場規定:當x<15時為不稱職,當15≤x<20時,為基本稱職,當20≤x<25為稱職,當x≥25時為優秀.則扇形統計圖中的a=________,b=________.
(2)所有營業員月銷售額的中位數和眾數分別是多少?
(3)為了調動營業員的積極性,決定制定一個月銷售額獎勵標準,凡到達或超過這個標準的營業員將受到獎勵.如果要使得營業員的半數左右能獲獎,獎勵標準應定為多少萬元?并簡述其理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某國際化學校實行小班制教學,七年級四個班共有學生(6m-3n)人,一班有學生m人,二班人數比一班人數的兩倍少n人,三班人數比二班人數的一半多12人.
(1)求三班的學生人數(用含m.n的式子表示);
(2)求四班的學生人數;(用含m.n的式子表示);
(3)若四個班共有學生120人,求二班比三班多的學生人數?
查看答案和解析>>
科目:初中數學 來源: 題型:
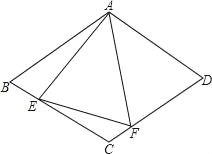
【題目】如圖,在菱形ABCD中,AB=4,∠BAD=120°,△AEF為正三角形,E、F在菱形的邊BC,CD上.
(1)證明:BE=CF.
(2)當點E,F分別在邊BC,CD上移動時(△AEF保持為正三角形),請探究四邊形AECF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
(3)在(2)的情況下,請探究△CEF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() ,
,![]() 上,連接
上,連接![]() .
.
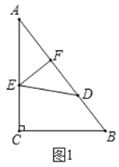
(1)將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,如圖1,若
處,如圖1,若![]() ,求
,求![]() 的長;
的長;
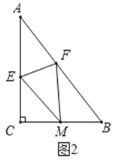
(2)將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,如圖2,若
處,如圖2,若![]() .
.
①求![]() 的長;
的長;
②求四邊形![]() 的面積;
的面積;
(3)若點![]() 在射線
在射線![]() 上,點
上,點![]() 在邊
在邊![]() 上,點
上,點![]() 關于
關于![]() 所在直線的對稱點為點
所在直線的對稱點為點![]() ,問:是否存在以
,問:是否存在以![]() 、
、![]() 為對邊的平行四邊形,若存在,求出
為對邊的平行四邊形,若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖直線y=2x+m與y=![]() (n≠0)交于A,B兩點,且點A的坐標為(1,4).
(n≠0)交于A,B兩點,且點A的坐標為(1,4).
(1)求此直線和雙曲線的表達式;
(2)過x軸上一點M作平行于y軸的直線1,分別與直線y=2x+m和雙曲線y=![]() (n≠0)交于點P,Q,如果PQ=2QM,求點M的坐標.
(n≠0)交于點P,Q,如果PQ=2QM,求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AD∥BC,AC=BC=4,∠D=90°,M,N分別是AB、DC的中點,過B作BE⊥AC交射線AD于點E,BE與AC交于點F.
(1)當∠ACB=30°時,求MN的長:
(2)設線段CD=x,四邊形ABCD的面積為y,求y與x的函數關系式及其定義域;
(3)聯結CE,當CE=AB時,求四邊形ABCE的面積.
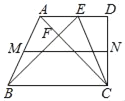
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC、BD相交于點G,E、F分別是邊AD、BC的中點,AB=2,BC=4,一動點P從點B出發,沿著B﹣A﹣D﹣C的方向在矩形的邊上運動,運動到點C停止.點M為圖1中的某個定點,設點P運動的路程為x,△BPM的面積為y,表示y與x的函數關系的圖象大致如圖2所示.那么,點M的位置可能是圖1中的( )
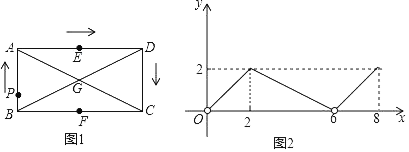
A. 點CB. 點EC. 點FD. 點G
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師設計了一個數學實驗,給甲、乙、丙三名同學各一張寫有已化為最簡(沒有同類項)的代數式的卡片,規則是兩位同學的代數式相減等于第三位同學的代數式,則實驗成功,甲、乙、丙的卡片如下,丙的卡片有一部分看不清楚了.
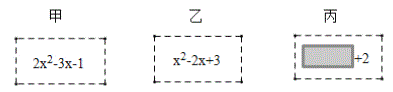
(1)計算出甲減乙的結果,并判斷甲減乙能否使實驗成功;
(2)嘉琪發現丙減甲可以使實驗成功,請求出丙的代數式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com