
【題目】如圖是某商品的標志圖案,AC與BD是⊙O的兩條直徑,首尾順次連接點A,B,C,D,得到四邊形ABCD.若AC=10cm,∠BAC=36°,則圖中陰影部分的面積為( ) 
A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
【答案】B
【解析】解:∵AC與BD是⊙O的兩條直徑, ∴∠ABC=∠ADC=∠DAB=∠BCD=90°,
∴四邊形ABCD是矩形,
∴△ABO于△CDO的面積=△AOD與△BOD 的面積,
∴圖中陰影部分的面積=S扇形AOD+S扇形BOC=2S扇形AOD ,
∵OA=OB,
∴∠BAC=∠ABO=36°,
∴∠AOD=72°,
∴圖中陰影部分的面積=2× ![]() =10π,
=10π,
故選B.
【考點精析】本題主要考查了圓周角定理和扇形面積計算公式的相關知識點,需要掌握頂點在圓心上的角叫做圓心角;頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角;一條弧所對的圓周角等于它所對的圓心角的一半;在圓上,由兩條半徑和一段弧圍成的圖形叫做扇形;扇形面積S=π(R2-r2)才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如果∠A和∠B互補,且∠A>∠B,給出下列四個式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.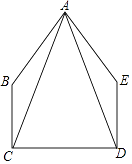
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小黃準備給長8m,寬6m的長方形客廳鋪設瓷磚,現將其劃分成一個長方形ABCD區域Ⅰ(陰影部分)和一個環形區域Ⅱ(空白部分),其中區域Ⅰ用甲、乙、丙三種瓷磚鋪設,且滿足PQ∥AD,如圖所示.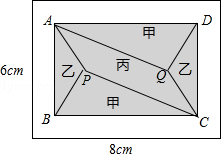
(1)若區域Ⅰ的三種瓷磚均價為300元/m2 , 面積為S(m2),區域Ⅱ的瓷磚均價為200元/m2 , 且兩區域的瓷磚總價為不超過12000元,求S的最大值;
(2)若區域Ⅰ滿足AB:BC=2:3,區域Ⅱ四周寬度相等
①求AB,BC的長;
②若甲、丙兩瓷磚單價之和為300元/m2 , 乙、丙瓷磚單價之比為5:3,且區域Ⅰ的三種瓷磚總價為4800元,求丙瓷磚單價的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD和四邊形DEFG都是正方形,點E,G分別在AD,CD上,連接AF,BF,CF.
(1)求證:AF=CF;
(2)若∠BAF=35°,求∠BFC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD=CD,∠ABD=∠ACD=90°,點E、F分別在AB、AC上,若ED平分∠BEF.
(1)求證:FD平分∠EFC.
(2)若EF=4,AF=6,AE=5,求BE和CF的和的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】”切實減輕學生課業負擔”是我市作業改革的一項重要舉措.某中學為了解本校學生平均每天的課外作業時間,隨機抽取部分學生進行問卷調查,并將調查結果分為A、B、C、D四個等級,A:1小時以內;B:1小時﹣﹣1.5小時;C:1.5小時﹣﹣2小時;D:2小時以上.根據調查結果繪制了如圖所示的兩種不完整的統計圖, 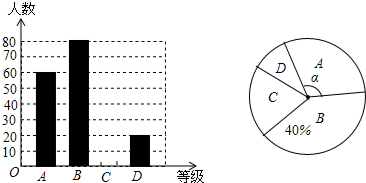
請根據圖中信息解答下列問題:
(1)該校共調查了學生;
(2)請將條形統計圖補充完整;
(3)表示等級A的扇形圓心角α的度數是;
(4)在此次調查問卷中,甲、乙兩班各有2人平均每天課外作業量都是2小時以上,從這4人中人選2人去參加座談,用列表表或畫樹狀圖的方法求選出的2人來自不同班級的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com