
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為直徑作
為直徑作![]() 交
交![]() 于點
于點![]() ,
,![]() 是
是![]() 的中點,連接
的中點,連接![]() .點
.點![]() 在
在![]() 上,連接
上,連接![]() 并延長交
并延長交![]() 的延長線于點
的延長線于點![]() .
.
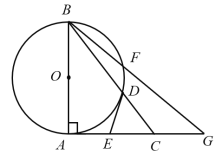
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)連接![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)見解析;(2)![]()
【解析】
(1)連接OD,AD.根據圓周角定理得到∠ADB=90°,求得∠ADC=90°,根據線段中點的定義得到DE=AE,求得∠EAD=∠EDA,根據等腰三角形的性質得到∠OAD=∠ODA,推出OD⊥DE,于是得到結論;
(2)過點F作FH⊥AB于點H,連接OF,得到∠AHF=90°.根據余角的想性質得到∠G=∠BAF,根據相似三角形的性質得到![]() ,由垂線段最短可得FH≤OF,當且僅當點H,O重合時等號成立.于是得到結論.
,由垂線段最短可得FH≤OF,當且僅當點H,O重合時等號成立.于是得到結論.
(1)證明:連接![]() ,
,![]() .
.
∵![]() 為
為![]() 直徑,點
直徑,點![]() 在
在![]() 上,
上,

∴![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中點,
的中點,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
∵![]() 是半徑
是半徑![]() 的外端點,
的外端點,
∴![]() 是
是![]() 的切線.
的切線.
(2)過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,
,
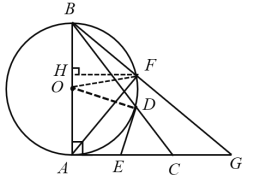
∴![]() .
.
∵![]() 為
為![]() 直徑,點
直徑,點![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
由垂線段最短可得![]() ,
,
當且僅當點![]() ,
,![]() 重合時等號成立.
重合時等號成立.
∵![]() ,
,
∴![]() 上存在點
上存在點![]() 使得
使得![]() ,此時點
,此時點![]() ,
,![]() 重合,
重合,
∴![]() ,
,
即![]() 的最大值為
的最大值為![]() .
.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】將一個矩形紙片![]() 放置在平面直角坐標系中,點
放置在平面直角坐標系中,點![]() ,點
,點![]() ,點E,F分別在邊
,點E,F分別在邊![]() ,
,![]() 上.沿著
上.沿著![]() 折疊該紙片,使得點A落在
折疊該紙片,使得點A落在![]() 邊上,對應點為
邊上,對應點為![]() ,如圖①.再沿
,如圖①.再沿![]() 折疊,這時點E恰好與點C重合,如圖②.
折疊,這時點E恰好與點C重合,如圖②.

(Ⅰ)求點C的坐標;
(Ⅱ)將該矩形紙片展開,再折疊該矩形紙片,使點O與點F重合,折痕與![]() 相交于點P,展開矩形紙片,如圖③.
相交于點P,展開矩形紙片,如圖③.
①求![]() 的大小;
的大小;
②點M,N分別為![]() ,
,![]() 上的動點,當
上的動點,當![]() 取得最小值時,求點N的坐標(直接寫出結果即可).
取得最小值時,求點N的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
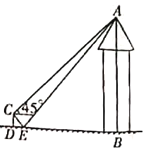
【題目】某次臺風來襲時,一棵筆直大樹樹干AB(假定樹干AB垂直于水平地面)被刮傾斜7°(即∠BAB′=7°)后折斷倒在地上,樹的頂部恰好接觸到地面D處,測得∠CDA=37°,AD=5米,求這棵大樹AB的高度.(結果保留根號)(參考數據:sin37≈0.6,cos37=0.8,tan37≈0.75)
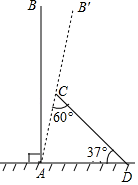
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源,生活垃圾一般按如圖所示A、B、C、D四種分類方法回收處理,某城市環保部門為了提高宣傳實效,抽樣調查、統計了部分居民小區一段時間內生活垃圾的分類處理情況,并將調查統計結果繪制成如下兩幅不完整的統計圖表:
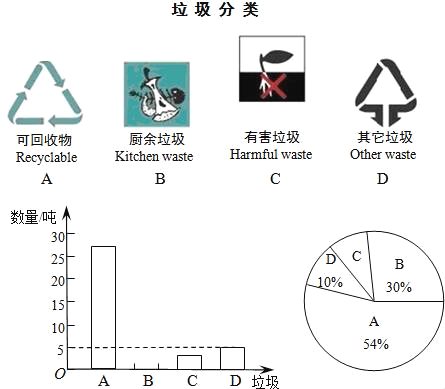
根據圖表解答下列問題:
(1)請將條形統計圖補充完整;
(2)在抽樣數據中,產生的有害垃圾共 噸;
(3)調查發現,在可回收物中塑料類垃圾占![]() ,每回收1噸塑料類垃圾可獲得0.7噸二級原料.假設該城市每月產生的生活垃圾為5000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
,每回收1噸塑料類垃圾可獲得0.7噸二級原料.假設該城市每月產生的生活垃圾為5000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮和小剛利用學過的測量知識測量一座房子的高度,如圖所示,他們先在地面上的點![]() 處豎直放了一根標桿
處豎直放了一根標桿![]() ,在房子和標桿之間的地面上平放一平面鏡,并在鏡面上做了一個標記,小剛來回移動平面鏡,當這個標記與地面上的點
,在房子和標桿之間的地面上平放一平面鏡,并在鏡面上做了一個標記,小剛來回移動平面鏡,當這個標記與地面上的點![]() 重合時,小亮在標桿頂端
重合時,小亮在標桿頂端![]() 處剛好看到房子的頂端點
處剛好看到房子的頂端點![]() 在鏡面中的像與鏡面上的標記重合,此時,在
在鏡面中的像與鏡面上的標記重合,此時,在![]() 處測得房子頂端點
處測得房子頂端點![]() 的仰角為
的仰角為![]() ,點
,點![]() 到點
到點![]() 的距離為0.8米.標桿
的距離為0.8米.標桿![]() 的長度為1米,已知點
的長度為1米,已知點![]() 在同一水平直線上,且
在同一水平直線上,且![]() 均垂直于
均垂直于![]() ,求房子的高度
,求房子的高度![]() (平面鏡的厚度忽略不計)
(平面鏡的厚度忽略不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊AD⊥y軸,垂足為點E,頂點A在第二象限,頂點B在y軸的正半軸上,反比例函數y=![]() (k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.
(k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
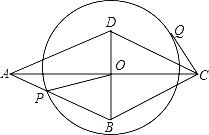
【題目】如圖:已知菱形ABCD中,對角線AC和BD相交于點O,AC=8,BD=6,動點P在邊AB上運動,以點O為圓心,OP為半徑作⊙O,CQ切⊙O于點Q.則在點P運動過程中,切線CQ的長的最大值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
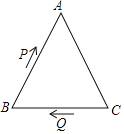
【題目】如圖,在△ABC中,AB=AC=8,BC=6,點P從點B出發以1個單位/s的速度向點A運動,同時點Q從點C出發以2個單位/s的速度向點B運動.當以B,P,Q為頂點的三角形與△ABC相似時,運動時間為( )
A.![]() sB.
sB.![]() sC.
sC.![]() s或
s或![]() sD.以上均不對
sD.以上均不對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com