
【題目】二次函數y=ax2+bx+c的圖象如圖所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,則P,Q的大小關系是 . 
【答案】P>Q
【解析】解:∵拋物線的開口向下,
∴a<0,
∵﹣ ![]() >0,
>0,
∴b>0,
∴2a﹣b<0,
∵﹣ ![]() =1,
=1,
∴b+2a=0,
x=﹣1時,y=a﹣b+c<0.
∴﹣ ![]() b﹣b+c<0,
b﹣b+c<0,
∴3b﹣2c>0,
∵拋物線與y軸的正半軸相交,
∴c>0,
∴3b+2c>0,
∴p=3b﹣2c,
Q=b﹣2a﹣3b﹣2c=﹣2a﹣2b﹣2c,
∴Q﹣P=﹣2a﹣2b﹣2c﹣3b+2c=﹣2a﹣5b=﹣4b<0
∴P>Q,
所以答案是:P>Q.
【考點精析】認真審題,首先需要了解二次函數的性質(增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小),還要掌握二次函數圖象以及系數a、b、c的關系(二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c))的相關知識才是答題的關鍵.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,點F在邊AC上,并且CF=1,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是 . 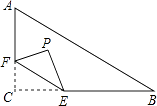
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“知識改變命運,科技繁榮祖國”.某區中小學每年都要舉辦一屆科技比賽.如圖為某區某校2015年參加科技比賽(包括電子百拼、航模、機器人、建模四個類別)的參賽人數統計圖: 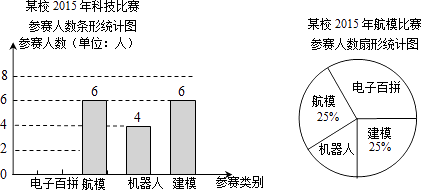
(1)該校參加機器人、建模比賽的人數分別是人和人;
(2)該校參加科技比賽的總人數是人,電子百拼所在扇形的圓心角的度數是°,并把條形統計圖補充完整.
(3)從全區中小學參加科技比賽選手中隨機抽取85人,其中有34人獲獎.2015年某區中小學參加科技比賽人數共有3625人,請你估算2015年參加科技比賽的獲獎人數約是多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點F在ABCD的對角線AC上,過點F、B分別作AB、AC的平行線相交于點E,連接BF,∠ABF=∠FBC+∠FCB. 
(1)求證:四邊形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE= ![]() ,求AC的長.
,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正確的個數是( ) 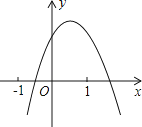
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y=ax2+bx的圖象過點A(﹣1,3),頂點B的橫坐標為1.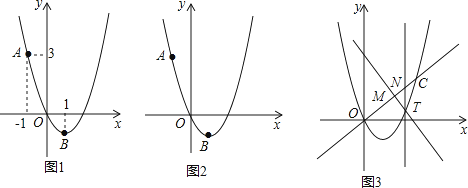
(1)求這個二次函數的表達式;
(2)點P在該二次函數的圖象上,點Q在x軸上,若以A、B、P、Q為頂點的四邊形是平行四邊形,求點P的坐標;
(3)如圖3,一次函數y=kx(k>0)的圖象與該二次函數的圖象交于O、C兩點,點T為該二次函數圖象上位于直線OC下方的動點,過點T作直線TM⊥OC,垂足為點M,且M在線段OC上(不與O、C重合),過點T作直線TN∥y軸交OC于點N.若在點T運動的過程中, ![]() 為常數,試確定k的值.
為常數,試確定k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以x為自變量的二次函數y=x2﹣2(b﹣2)x+b2﹣1的圖象不經過第三象限,則實數b的取值范圍是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形ABOC的兩邊在坐標軸上,OB=1,點A在函數y=﹣ ![]() (x<0)的圖象上,將此矩形向右平移3個單位長度到A1B1O1C1的位置,此時點A1在函數y=
(x<0)的圖象上,將此矩形向右平移3個單位長度到A1B1O1C1的位置,此時點A1在函數y= ![]() (x>0)的圖象上,C1O1與此圖象交于點P,則點P的縱坐標是( )
(x>0)的圖象上,C1O1與此圖象交于點P,則點P的縱坐標是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從﹣3,﹣1, ![]() ,1,3這五個數中,隨機抽取一個數,記為a,若數a使關于x的不等式組
,1,3這五個數中,隨機抽取一個數,記為a,若數a使關于x的不等式組  無解,且使關于x的分式方程
無解,且使關于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整數解,那么這5個數中所有滿足條件的a的值之和是( )
=﹣1有整數解,那么這5個數中所有滿足條件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com