
【題目】某校開展校園“美德少年”評選活動,共有“助人為樂”,“自強自立”、“孝老愛親”,“誠實守信”四種類別,每位同學只能參評其中一類,評選后,把最終入選的20位校園“美德少年”分類統計,制作了如下統計表,后來發現,統計表中前兩行的數據都是正確的,后兩行的數據中有一個是錯誤的.
類別 | 頻數 | 頻率 |
助人為樂美德少年 | a | 0.20 |
自強自立美德少年 | 3 | b |
孝老愛親美德少年 | 7 | 0.35 |
誠實守信美德少年 | 6 | 0.32 |
根據以上信息,解答下列問題:
(1)統計表中的a= ,b ;
(2)統計表后兩行錯誤的數據是 ,該數據的正確值是 ;
(3)校園小記者決定從A,B,C三位“自強自立美德少年”中隨機采訪兩位,用畫樹狀圖或列表的方法,求A,B都被采訪到的概率.
 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩車從![]() 地出發,勻速駛向
地出發,勻速駛向![]() 地,甲車以
地,甲車以![]() 的速度行駛
的速度行駛![]() 后,乙車才沿相同路線行駛,乙車先到達
后,乙車才沿相同路線行駛,乙車先到達![]() 地并停留
地并停留![]() 后,再以原速沿原路返回,直至與甲車相遇.在此過程中,兩車之間的距離
后,再以原速沿原路返回,直至與甲車相遇.在此過程中,兩車之間的距離![]() 與乙車行駛時間
與乙車行駛時間![]() 之間的函數關系如圖所示,下列說法錯誤的是( )
之間的函數關系如圖所示,下列說法錯誤的是( )
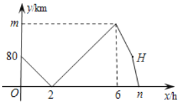
A.乙車的速度是![]() B.
B.![]()
C.點![]() 的坐標是
的坐標是![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,⊙O是正方形ABCD的外接圓,P是⊙O上不與A、B重合的任意一點,則∠APB等于( )
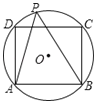
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“武漢加油!中國加油!”疫情牽動萬人心,每個人都在為抗擊疫情而努力.某廠改造了![]() 條口罩生產線,每條生產線每天可生產口罩
條口罩生產線,每條生產線每天可生產口罩![]() 個.如果每增加一條生產線,每條生產線就會比原來少生產
個.如果每增加一條生產線,每條生產線就會比原來少生產![]() 個口罩.設增加
個口罩.設增加![]() 條生產線后,每條生產線每天可生產口罩
條生產線后,每條生產線每天可生產口罩![]() 個.
個.
![]() 直接寫出
直接寫出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
![]() 若每天共生產口罩
若每天共生產口罩![]() 個,在投入人力物力盡可能少的情況下,應該增加幾條生產線?
個,在投入人力物力盡可能少的情況下,應該增加幾條生產線?
![]() 設該廠每天可以生產的口罩
設該廠每天可以生產的口罩![]() 個,請求出
個,請求出![]() 與
與![]() 的函數關系式,并求出增加多少條生產線時,每天生產的口罩數量最多,最多為多少個?
的函數關系式,并求出增加多少條生產線時,每天生產的口罩數量最多,最多為多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
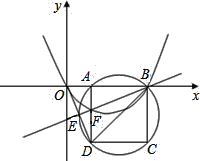
【題目】如圖,在平面直角坐標系中,已知點![]() 、
、![]() ,以
,以![]() 為邊在
為邊在![]() 軸下方作正方形
軸下方作正方形![]() ,點
,點![]() 是線段
是線段![]() 與正方形
與正方形![]() 的外接圓的交點,連接
的外接圓的交點,連接![]() 與
與![]() 相交于點
相交于點![]() .
.
(1)求證:![]() ;
;
(2)若![]() ,試求經過
,試求經過![]() 、
、![]() 、
、![]() 三點的拋物線
三點的拋物線![]() 的解析式;
的解析式;
(3)在(2)的條件下,將拋物線![]() 在
在![]() 軸下方的部分沿
軸下方的部分沿![]() 軸翻折,圖象的其余部分保持不變,得到一個新圖象,若直線
軸翻折,圖象的其余部分保持不變,得到一個新圖象,若直線![]() 向上平移t個單位與新圖象有兩個公共點,試求t的取值范圍.
向上平移t個單位與新圖象有兩個公共點,試求t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
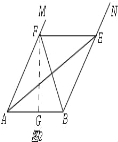
【題目】如圖,已知四邊形ABCD和四邊形DEFG為正方形,點E在線段DE上,點A,D,G在同一直線上,且AD=3,DE=1,連接AC,CG,AE,并延長AE交CG于點H.
(1)求sin∠EAC的值.
(2)求線段AH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成一件事有幾類辦法,各類辦法相互獨立,每類辦法中又有多種不同的辦法,則完成這件事的不同辦法數是各類不同方法種數的和,這就是分類計數原理,也叫做加法原理.完成一件事,需要分成幾個步驟,每一步的完成有多種不同的方法,則完成這件事的不同方法種數是各種不同的方法數的乘積,這就是分步計數原理,也叫做乘法原理.
小王同學參加某高中學校進行的自主招生考試,本次考試共有1000人參加.
(1)1000人參加自招考試,有300人可以享受加分政策,且有10,20,30,60四個檔次,小王想獲得至少30分的加分,那么概率為多少?
(2)若該高中的中考錄取分數線為530分,小王估得中考分數可能在500-509,510-519,520-529三個分段,
①若小王的中考分數在510~519分段,則小王被該高中錄取的概率為多少?
②若小王的中考分數在三個分數段對應的概率分別為![]() ,
,![]() ,
,![]() ,則小王被該高中錄取的概率為多少?
,則小王被該高中錄取的概率為多少?
加分 | 人數 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com