
【題目】如圖,頂點為M的拋物線y=ax2+bx+3與x軸交于A(3,0),B(﹣1,0)兩點,與y軸交于點C
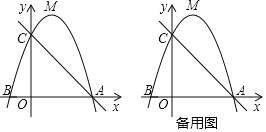
(1)求拋物線的表達式;
(2)在直線AC的上方的拋物線上,有一點P(不與點M重合),使△ACP的面積等于△ACM的面積,請求出點P的坐標;
(3)在y軸上是否存在一點Q,使得△QAM為直角三角形?若存在,請直接寫出點Q的坐標:若不存在,請說明理由.
【答案】(1)y=﹣x2+2x+3;(2)點P的坐標為:(2,3);(3)存在,點Q的坐標為:(0,1)或(0,3)或(0,![]() )或(0,﹣
)或(0,﹣![]() )
)
【解析】
(1)拋物線的表達式為:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;
(2)過點M作直線m∥AC,在AC下方作等距離的直線n,直線n與拋物線交點即為點P,即可求解;
(3)分AM時斜邊、AQ是斜邊、MQ是斜邊三種情況,分別求解即可.
解:(1)拋物線的表達式為:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=1,解得:a=﹣1,
故拋物線的表達式為:y=﹣x2+2x+3;
(2)過點M作直線m∥AC,直線m與拋物線交點即為點P,
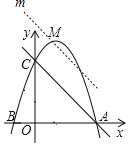
設直線m的表達式為:y=﹣x+b,
點M(1,4),則直線m的表達式為:y=﹣x+5,
聯(lián)立方程組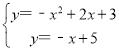 ,
,
解得:x=1(舍去)或2;
故點P的坐標為:(2,3);
(3)設點Q的坐標為:(0,m),而點A、M的坐標分別為:(3,0)、(1,4);
則AM2=20,AQ2=9+m2,MQ2=(m﹣4)2+1=m2﹣8m+17;
當AM時斜邊時,則20=9+m2+m2﹣8m+17,解得:m=1或3;
當AQ是斜邊時,則9+m2=20+ m2﹣8m+17,解得m=![]() ;
;
當MQ是斜邊時,則m2﹣8m+17=20+9+m2,解得m=﹣![]() ,
,
綜上,點Q的坐標為:(0,1)或(0,3)或(0,![]() )或(0,﹣
)或(0,﹣![]() )
)


 小學課堂作業(yè)系列答案
小學課堂作業(yè)系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數(shù)學 來源: 題型:
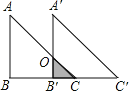
【題目】如圖所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,現(xiàn)將△ABC沿BC方向平移到△A′B′C′的位置.若平移的距離為3,則△ABC與△A′B′C′重疊部分的陰影面積為__.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
(1) 請畫出△ABC向左平移5個單位長度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 請畫出△ABC關于原點對稱的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.
軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,⊙O經(jīng)過點A、C、D,與BC相交于點E,連接AC、AE.若∠D=70°,則∠EAC的度數(shù)為____________.
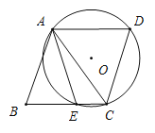
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
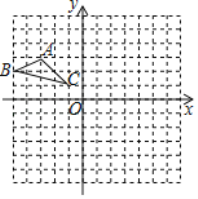
【題目】△ABC在邊長為l的正方形網(wǎng)格中如圖所示.
①以點C為位似中心,作出△ABC的位似圖形△A1B1C,使其位似比為1:2.且△A1B1C位于點C的異側,并表示出A1的坐標.
②作出△ABC繞點C順時針旋轉90°后的圖形△A2B2C.
③在②的條件下求出點B經(jīng)過的路徑長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
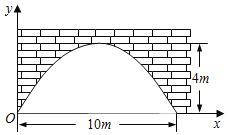
【題目】有一個拋物線形的拱形橋洞,橋洞離水面的最大高度為4m,跨度為10m,如圖所示,把它的圖形放在直角坐標系中.
(1)求這條拋物線所對應的函數(shù)關系式;
(2)一輛寬為2米,高為3米的貨船能否從橋下通過?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
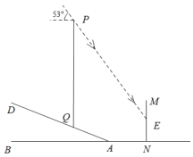
【題目】重慶移動為了提升新型冠狀肺炎“停課不停學”期間某片區(qū)網(wǎng)絡信號,保證廣大師生網(wǎng)絡授課、聽課的質量,臨時在坡度為![]() 的山坡上加裝了信號塔
的山坡上加裝了信號塔![]() (如圖所示),信號塔底端
(如圖所示),信號塔底端![]() 到坡底
到坡底![]() 的距離為3.9米.同時為了提醒市民,在距離斜坡底4.4米的水平地面上立了一塊警示牌
的距離為3.9米.同時為了提醒市民,在距離斜坡底4.4米的水平地面上立了一塊警示牌![]() .當太陽光線與水平線成53°角時,測得信號塔
.當太陽光線與水平線成53°角時,測得信號塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 長為3米,則信號塔
長為3米,則信號塔![]() 的高約為(tan53°≈1.3)( ).
的高約為(tan53°≈1.3)( ).
A.10.4B.11.9C.11.4D.13.4
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
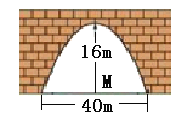
【題目】如圖,有一拋物線型的立交橋橋拱,這個橋拱的最大高度為16米,跨度為40米,若要在跨度中心點![]() 的左,右5米處各垂直豎立一根鐵柱支撐拱頂,則鐵柱應取多長?
的左,右5米處各垂直豎立一根鐵柱支撐拱頂,則鐵柱應取多長?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
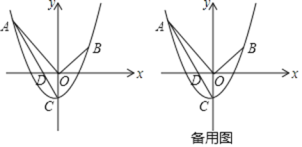
【題目】如圖,在平面直角坐標系中,拋物線![]() ,過點
,過點![]() 和點
和點![]() ,與y軸交于點C,連接AC交x軸于點D,連接OA,OB
,與y軸交于點C,連接AC交x軸于點D,連接OA,OB
![]() 求拋物線
求拋物線![]() 的函數(shù)表達式;
的函數(shù)表達式;
![]() 求點D的坐標;
求點D的坐標;
![]() 的大小是______;
的大小是______;
![]() 將
將![]() 繞點O旋轉,旋轉后點C的對應點是點
繞點O旋轉,旋轉后點C的對應點是點![]() ,點D的對應點是點
,點D的對應點是點![]() ,直線
,直線![]() 與直線
與直線![]() 交于點M,在
交于點M,在![]() 旋轉過程中,當點M與點
旋轉過程中,當點M與點![]() 重合時,請直接寫出點M到AB的距離.
重合時,請直接寫出點M到AB的距離.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com