
【題目】對于⊙C與⊙C上的一點A,若平面內的點P滿足:射線AP與⊙C交于點Q(點Q可以與點P重合),且![]() ,則點P稱為點A關于⊙C的“生長點”.
,則點P稱為點A關于⊙C的“生長點”.
已知點O為坐標原點,⊙O的半徑為1,點A(-1,0).
(1)若點P是點A關于⊙O的“生長點”,且點P在x軸上,請寫出一個符合條件的點P的坐標________;
(2)若點B是點A關于⊙O的“生長點”,且滿足![]() ,求點B的縱坐標t的取值范圍;
,求點B的縱坐標t的取值范圍;
(3)直線![]() 與x軸交于點M,與y軸交于點N,若線段MN上存在點A關于⊙O的“生長點”,直接寫出b的取值范圍是_____________________________.
與x軸交于點M,與y軸交于點N,若線段MN上存在點A關于⊙O的“生長點”,直接寫出b的取值范圍是_____________________________.
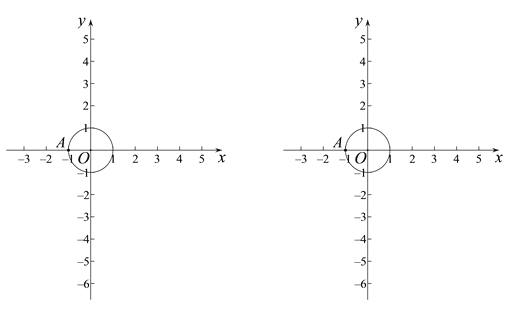
【答案】(1)(2,0)(答案不唯一);(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】試題分析:
(1)由題意可知,在x軸上找點P是比較簡單的,這樣的P點不是唯一的,如點(2,0)、(1,0)等;
(2)如圖1,在x軸上方作射線AM交⊙O于點M,使tan∠MAO=![]() ,并在射線AM是取點N,使MN=AM,則由題意可知,線段MN上的點都是符合條件的B點,過點M作MH⊥x軸于點H,連接MC,結合已知條件求出點M和點N的縱坐標即可得到所求B點的縱坐標t的取值范圍;根據對稱性,在x軸的下方得到線段M′N′,同理可求得滿足條件的B點的縱坐標t的另一取值范圍;
,并在射線AM是取點N,使MN=AM,則由題意可知,線段MN上的點都是符合條件的B點,過點M作MH⊥x軸于點H,連接MC,結合已知條件求出點M和點N的縱坐標即可得到所求B點的縱坐標t的取值范圍;根據對稱性,在x軸的下方得到線段M′N′,同理可求得滿足條件的B點的縱坐標t的另一取值范圍;
(3)如圖2,3,由![]() 與x軸交于點M,與y軸交于點N,可得點M的坐標為
與x軸交于點M,與y軸交于點N,可得點M的坐標為![]() ,點N的坐標為
,點N的坐標為![]() ,由此結合∠OMN的正切函數可求得∠OMN=60°;
,由此結合∠OMN的正切函數可求得∠OMN=60°;
以點D(1,0)為圓心,2為半徑作圓⊙D,則⊙D和⊙O相切于點A,由題意可知,點A關于⊙O的“生長點”都在⊙O到⊙D之間的平面內,包括兩個圓(但點A除外).
然后結合題意和∠OMN=60°分b>0和b<0兩種情況在圖2和圖3中求出ON1和ON2的長即可得到b的取值范圍了.
試題解析:
(1)由題意可知,在x軸上找點P是比較簡單的,這樣的P點不是唯一的,如點(2,0)、(1,0)等;
(2)如圖1,在x軸上方作射線AM,與⊙O交于M,且使得![]() ,并在AM上取點N,使AM=MN,并由對稱性,將MN關于x軸對稱,得
,并在AM上取點N,使AM=MN,并由對稱性,將MN關于x軸對稱,得![]() ,則由題意,線段MN和
,則由題意,線段MN和![]() 上的點是滿足條件的點B.
上的點是滿足條件的點B.
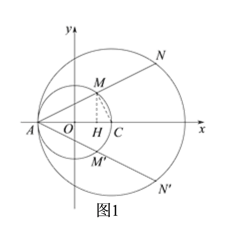
作MH⊥x軸于H,連接MC,
∴ ∠MHA=90°,即∠OAM+∠AMH=90°.
∵ AC是⊙O的直徑,
∴ ∠AMC=90°,即∠AMH+∠HMC=90°.
∴ ∠OAM=∠HMC.
∴![]() .
.
∴![]() .
.
設![]() ,則
,則![]() ,
, ![]() ,
,
∴![]() ,解得
,解得![]() ,即點M的縱坐標為
,即點M的縱坐標為![]() .
.
又由![]() ,A為(-1,0),可得點N的縱坐標為
,A為(-1,0),可得點N的縱坐標為![]() ,
,
故在線段MN上,點B的縱坐標t滿足: ![]() .
.
由對稱性,在線段![]() 上,點B的縱坐標t滿足:
上,點B的縱坐標t滿足: ![]() .
.
∴ 點B的縱坐標t的取值范圍是![]() 或
或![]() .
.
(3)如圖2,以點D(1,0)為圓心,2為半徑作圓⊙D,則⊙D和⊙O相切于點A,由題意可知,點A關于⊙O的“生長點”都在⊙O到⊙D之間的平面內,包括兩個圓(但點A除外).
∵直線![]() 與x軸交于點M,與y軸交于點N,
與x軸交于點M,與y軸交于點N,
∴點M的坐標為![]() ,點N的坐標為
,點N的坐標為![]() ,
,
∴tan∠OMN=![]() ,
,
∴∠OMN=60°,
要在線段MN上找點A關于⊙O的“生長點”,現分“b>0”和“b<0”兩種情況討論:
I、①當直線![]() 過點N1(0,1)時,線段MN上有點A關于⊙O的唯一“生長點”N1,此時b=1;
過點N1(0,1)時,線段MN上有點A關于⊙O的唯一“生長點”N1,此時b=1;
②當直線![]() 與⊙D相切于點B時,線段MN上有點A關于⊙O的唯一“生長點”B,此時直線
與⊙D相切于點B時,線段MN上有點A關于⊙O的唯一“生長點”B,此時直線![]() 與y軸相交于點N2,與x軸相交于點M2,連接DB,則DB=2,
與y軸相交于點N2,與x軸相交于點M2,連接DB,則DB=2,
∴DM2=![]() ,
,
∴OM2=![]() ,
,
∴ON2=tan60°·OM2=![]() ,此時b=
,此時b=![]() .
.
綜合①②可得,當b>0時,若線段MN上存在點A關于⊙O的“生長點”,則b的取值范圍為: ![]() ;
;
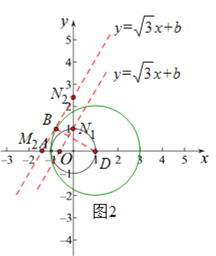
II、當b<0時,如圖3,同理可得若線段MN上存在點A關于⊙O的“生長點”,則b的取值范圍為: ![]() ;
;
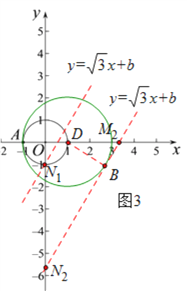
綜上所述,若在線段MN上存在點A關于⊙O的“生長點”,則b的取值范圍為: ![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,將函數y=![]() (x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )
(x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖點P是△ABC的邊BC上的一動點,點E與點P關于直線AB成軸對稱,連接EP交AB于點F,連接AP、EC相交于點O,連接AE.

(1)判斷AE與AP的數量關系,并說明理由.
(2)在點P的運動過程中,當AE∥BC時,判斷AP與BP的數量關系,并說明理由.
(3)若∠BAC=900,點P在運動過程中是否存在線段AP與線段EC互相平分的情況,若存在,請求出點P的位置;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個少年在綠茵場上游戲.小紅從點A出發沿線段AB運動到點B,小蘭從點C出發,以相同的速度沿⊙O逆時針運動一周回到點C,兩人的運動路線如圖1所示,其中AC![]() DB.兩人同時開始運動,直到都停止運動時游戲結束,其間他們與點C的距離y與時間x(單位:秒)的對應關系如圖2所示.則下列說法正確的是( )
DB.兩人同時開始運動,直到都停止運動時游戲結束,其間他們與點C的距離y與時間x(單位:秒)的對應關系如圖2所示.則下列說法正確的是( )


A. 小紅的運動路程比小蘭的長
B. 兩人分別在1.09秒和7.49秒的時刻相遇
C. 當小紅運動到點D的時候,小蘭已經經過了點D
D. 在4.84秒時,兩人的距離正好等于⊙O的半徑
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫圖,探究:
(1)一個正方體組合圖形的主視圖、左視圖(如圖1)所示.
①這個幾何體可能是(圖2)甲、乙中的 ;
②這個幾何體最多可由 個小正方體構成,請在圖3中畫出符合最多情況的一個俯視圖.
(2)如圖,已知一平面內的四個點A、B、C、D,根據要求用直尺畫圖.
①畫線段AB,射線AD;
②找一點M,使M點即在射線AD上,又在直線BC上;
③找一點N,使N到A、B、C、D四個點的距離和最短.


查看答案和解析>>
科目:初中數學 來源: 題型:
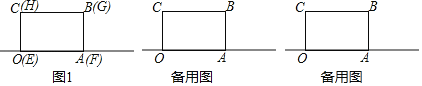
【題目】有兩個大小完全一樣的長方形OABC和EFGH重合放在一起,邊OA、EF在數軸上,O為數軸原點(如圖1),長方形OABC的邊長OA的長為6個坐標單位.
(1)數軸上點A表示的數為 .
(2)將長方形EFGH沿數軸所在直線水平移動
①若移動后的長方形EFGH與長方形OABC重疊部分的面積恰好等于長方形OABC面積的![]() ,則移動后點F在數軸上表示的數為 .
,則移動后點F在數軸上表示的數為 .
②若出行EFGH向左水平移動后,D為線段AF的中點,求當長方形EFGH移動距離x為何值時,D、E兩點在數軸上表示的數是互為相反數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 分別與x軸、y軸交于
分別與x軸、y軸交于![]() 兩點,與直線
兩點,與直線![]() 交于點C(4,2).
交于點C(4,2).
(1)點A坐標為( , ),B為( , );
(2)在線段![]() 上有一點E,過點E作y軸的平行線交直線
上有一點E,過點E作y軸的平行線交直線![]() 于點F,設點E的橫坐標為m,當m為何值時,四邊形
于點F,設點E的橫坐標為m,當m為何值時,四邊形![]() 是平行四邊形;
是平行四邊形;
(3)若點P為x軸上一點,則在平面直角坐標系中是否存在一點Q,使得![]() 四個點能構成一個菱形.若存在,求出所有符合條件的Q點坐標;若不存在,請說明理由.
四個點能構成一個菱形.若存在,求出所有符合條件的Q點坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P從(0,2)出發,沿所示的方向運動,每當碰到矩形的邊時反彈,反彈時反射角等于入射角,當點P第2019次碰到矩形的邊時點P的坐標為( )
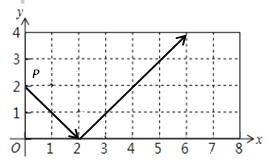
A.( 2,4 )B.( 2,0 )C.( 8,2)D.( 6,0 )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知n邊形的內角和θ=(n﹣2)×180°.
(1)甲同學說,θ能取900°;而乙同學說,θ也能取800°.甲、乙的說法對嗎?若對,求出邊數n.若不對,說明理由;
(2)若n邊形變為(n+x)邊形,發現內角和增加了540°,用列方程的方法確定x.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com