
【題目】如圖,直線![]() 分別與x軸、y軸交于
分別與x軸、y軸交于![]() 兩點,與直線
兩點,與直線![]() 交于點C(4,2).
交于點C(4,2).
(1)點A坐標為( , ),B為( , );
(2)在線段![]() 上有一點E,過點E作y軸的平行線交直線
上有一點E,過點E作y軸的平行線交直線![]() 于點F,設點E的橫坐標為m,當m為何值時,四邊形
于點F,設點E的橫坐標為m,當m為何值時,四邊形![]() 是平行四邊形;
是平行四邊形;
(3)若點P為x軸上一點,則在平面直角坐標系中是否存在一點Q,使得![]() 四個點能構成一個菱形.若存在,求出所有符合條件的Q點坐標;若不存在,請說明理由.
四個點能構成一個菱形.若存在,求出所有符合條件的Q點坐標;若不存在,請說明理由.

【答案】(1)(8,0);(0,4).(2)故當![]() 時,四邊形
時,四邊形![]() 是平行四邊形;(3)Q點坐標為
是平行四邊形;(3)Q點坐標為![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由點C的坐標利用待定系數法即可求出直線l1的解析式,再分別令直線![]() 的解析式中
的解析式中![]() 求出對應的y、x值,即可得出點A、B的坐標;
求出對應的y、x值,即可得出點A、B的坐標;
(2)由點C的坐標利用待定系數法即可求出直線![]() 的解析式,結合點E的橫坐標即可得出點E、F的坐標,再根據平行四邊形的性質即可得出關于m的一元一次方程,解方程即可得出結論;
的解析式,結合點E的橫坐標即可得出點E、F的坐標,再根據平行四邊形的性質即可得出關于m的一元一次方程,解方程即可得出結論;
(3)分![]() 為邊和
為邊和![]() 為對角線兩種情況討論.當
為對角線兩種情況討論.當![]() 為邊時,根據菱形的性質找出點P的坐標,結合A、B的坐標即可得出點Q的坐標;當
為邊時,根據菱形的性質找出點P的坐標,結合A、B的坐標即可得出點Q的坐標;當![]() 為對角線時,根據三角形相似找出點P的坐標,再根據菱形對角線互相平分即可得出點Q的坐標.綜上即可得出結論.
為對角線時,根據三角形相似找出點P的坐標,再根據菱形對角線互相平分即可得出點Q的坐標.綜上即可得出結論.
解:(1)將點C(4,2)代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
∴直線![]() 為
為![]() .
.
令![]() 中
中![]() ,則
,則![]() ,
,
∴B(0,4);
令![]() 中
中![]() ,則
,則![]() ,
,
∴A(8,0).
(2)∵點C(4,2)是直線![]() 上的點,
上的點,
∴![]() ,解得:
,解得:![]() ,
,
∴直線![]() 為
為![]() .
.
∵點E的橫坐標為![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,即
,即![]() ,
,
解得:![]() .
.
故當![]() 時,四邊形
時,四邊形![]() 是平行四邊形.
是平行四邊形.
(3)假設存在.
以![]() 為頂點的菱形分兩種情況:
為頂點的菱形分兩種情況:
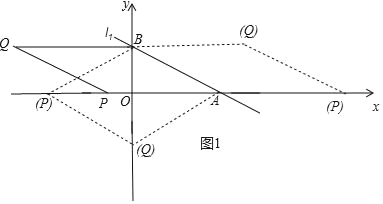
①以![]() 為邊,如圖1所示.
為邊,如圖1所示.
∵點A(8,0),B(0,4),
∴![]() .
.
∵以![]() 為頂點的四邊形為菱形,
為頂點的四邊形為菱形,
∴![]() 或
或![]() .
.
當![]() 時,
時,![]() 或
或![]() ;
;
當![]() 時,點P(﹣8,0).
時,點P(﹣8,0).
當![]() 時,
時,![]() ,即
,即![]() ;
;
當P(![]() )時,
)時,![]() ,即
,即![]() ;
;
當![]() 時,
時,![]() ,即
,即![]() .
.
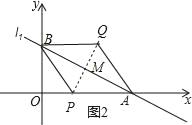
②以![]() 為對角線,對角線的交點為M,如圖2所示.
為對角線,對角線的交點為M,如圖2所示.
∵點![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴點![]() ,即(3,0).
,即(3,0).
∵以![]() 為頂點的四邊形為菱形,
為頂點的四邊形為菱形,
∴點![]() ,即(5,4).
,即(5,4).
綜上可知:若點P為x軸上一點,則在平面直角坐標系中存在一點Q,使得![]() 四個點能構成一個菱形,此時Q點坐標為
四個點能構成一個菱形,此時Q點坐標為![]() 、
、![]() 、
、![]() 或
或![]() .
.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:①四邊形CFHE是菱形;②EC平分∠DCH;③線段BF的取值范圍為3≤BF≤4;④當點H與點A重合時,EF=![]() .其中正確的結論是()
.其中正確的結論是()

A.①②③④B.①④C.①②④D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
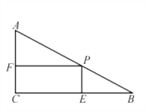
【題目】如圖,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,點P是AB邊上的一個動點,過點P作PE⊥BC于點E,PF⊥AC于點F,當PB=6cm時,四邊形PECF的面積最大,最大值為______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著中國傳統節日“端午節”的臨近,東方紅商場決定開展“歡度端午,回饋顧客”的讓利促銷活動,對部分品牌粽子進行打折銷售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,買6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,買50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙兩種品牌粽子每盒分別為多少元?
(2)陽光敬老院需購買甲品牌粽子80盒,乙品牌粽子100盒,問打折后購買這批粽子比不打折節省了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】函數y=ax2(a≠0)與直線y=2x-3的圖象交于點(1,b).
求:(1)a和b的值;
(2)求拋物線y=ax2的開口方向、對稱軸、頂點坐標;
(3)作y=ax2的草圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E、F、G、H分別為四邊形ABCD四邊之中點.
(1)求證:四邊形EFGH為平行四邊形;
(2)當AC、BD滿足 時,四邊形EFGH為菱形.當AC、BD滿足 時,四邊形EFGH為矩形.當AC、BD滿足 時,四邊形EFGH為正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社區購買甲、乙兩種樹苗進行綠化,購買一棵甲種樹苗的價錢比購買一棵乙種樹苗的價錢多 10 元錢,已知購買 20 棵甲種樹苗、30 棵乙種樹苗共需 1 200 元錢.
(1)求購買一棵甲種、一棵乙種樹苗各多少元?
(2)社區決定購買甲、乙兩種樹苗共 400 棵,總費用不超過 10 600 元,那么該社區最多可以購買多少棵甲種樹苗?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com