【題目】如圖，在直角坐標系內，O為原點，點A的坐標為(10，0)，點B在第一象限內，BO＝5，sin∠BOA＝
. 求：(1)點B的坐標；(2)cos∠BAO的值．
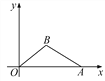
【答案】（1）點B的坐標為(4，3)；（2）cos∠BAO＝
.
【解析】試題分析：（1）作BH⊥OA， 垂足為H，在Rt△OHB中，根據銳角三角函數的定義及已知條件求得BH的長，再根據勾股定理求得OH的長，即可得點B的坐標；（2）先求得AH的長，在Rt△AHB中，根據勾股定理求得AB的長，根據銳角三角函數的定義即可求得cos∠BAO的值．
試題解析：
(1)如圖所示，作BH⊥OA， 垂足為H．
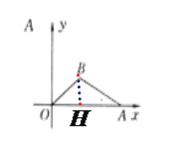
在Rt△OHB中，∵BO＝5，sin∠BOA＝
，∴BH=3，∴OH＝4，∴點B的坐標為(4，3)．
(2)∵OA＝10，OH＝4，∴AH＝6．在Rt△AHB中，∵BH=3，∴AB＝
，∴cos∠BAO=
= 
．
科目：初中數學 來源： 題型：
【題目】數學活動——探究特殊的平行四邊形．
問題情境
如圖，在四邊形ABCD中，AC為對角線，AB=AD，BC=DC．請你添加條件，使它們成為特殊的平行四邊形．
提出問題
（1）第一小組添加的條件是“AB∥CD”，則四邊形ABCD是菱形．請你證明；
（2）第二小組添加的條件是“∠B=90°,∠BCD=90°”，則四邊形ABCD是正方形．請你證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y=ax2+bx+c（a≠0）的圖象與x軸交于點A（﹣1，0），對稱軸為直線x=1，與y軸的交點B在（0，2）和（0，3）之間（包括這兩點），下列結論：
①當x＞3時，y＜0；②3a+b＜0；③﹣1≤a≤﹣
；④4ac﹣b2＞8a；
其中正確的結論是（ ）
A．①③④ B．①②③ C．①②④ D．①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某文具店準備購進A、B兩種型號的書包共50個進行銷售，兩種書包的進價、售價如下表所示：
書包型號 | 進價（元/個） | 售價（元/個） |
A型 | 200 | 300 |
B型 | 100 | 150 |
購進這50個書包的總費用不超過7300元，且購進B型書包的個數不大于A型書包個數的
．
（1）該文具店有哪幾種進貨方案？
（2）若該文具店購進的50個書包全部售完，則該文具店采用哪種進貨方案，才能獲得最大利潤？最大利潤是多少？（利潤＝售價﹣進價）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】超速行駛是引發交通事故的主要原因之一．上周末，小明和三位同學嘗試用自己所學的知識檢測車速．如圖，觀測點設在A處，離益陽大道的距離(AC)為30米．這時，一輛小轎車由西向東勻速行駛，測得此車從B處行駛到C處所用的時間為8秒，∠BAC＝75°.
(1)求B、C兩點的距離；
(2)請判斷此車是否超過了益陽大道60千米/小時的限制速度？
(計算時距離精確到1米，參考數據：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732， 
≈1.732，60千米/小時≈16.7米/秒)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平行四邊形ABCD中，點O是對角線BD中點，點E在邊BC上，EO的延長線與邊AD交于點F，連接BF、DE，如圖1．
（1）求證：四邊形BEDF是平行四邊形；
（2）在（1）中，若DE＝DC，∠CBD＝45°，過點C作DE的垂線，與DE、BD、BF分別交于點G、H、R，如圖2．
①當CD＝6，CE＝4時，求BE的長．
②探究BH與AF的數量關系，并給予證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】直角坐標系中，已知點P(－2，－1)，點T(t，0)是x軸上的一個動點.
(1)求點P關于原點的對稱點P′的坐標;
(2)當t取何值時，△P′TO是等腰三角形?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，攔水壩的橫斷面為等腰梯形ABCD，壩頂寬BC為6 m，壩高為3.2 m，為了提高水壩的攔水能力需要將水壩加高2 m，并且保持壩頂寬度不變，迎水坡CD的坡度不變，但是背水坡的坡度由原來的1∶2變成1∶2.5(坡度是坡高與坡的水平長度的比)．求加高后的壩底HD的長為多少．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐
閱讀以下材料：
定義：兩邊分別相等且夾角互補的兩個三角形叫做“互補三角形”．
用符號語言表示為：如圖①，在△ABC與△DEF中，如果AC=DE，∠C+∠E=180°，BC=EF，那么△ABC與△DEF是互補三角形．
反之，“如果△ABC與△DEF是互補三角形，那么有AC=DE，∠C+∠E=180°，BC=EF”也是成立的．
自主探究
利用上面所學知識以及全等三角形的相關知識解決問題：
（1）性質：互補三角形的面積相等
如圖②，已知△ABC與△DEF是互補三角形．
求證：△ABC與△DEF的面積相等．
證明：分別作△ABC與△DEF的邊BC，EF上的高線，則∠AGC=∠DHE=90°．
…… (將剩余證明過程補充完整)
（2）互補三角形一定不全等，請你判斷該說法是否正確，并說明理由，如果不正確，請舉出一個反例，畫出示意圖．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com