【題目】已知，如圖A、B分別為數軸上的兩點，A點對應的數為-10，B點對應的數為90．
（1）請寫出與A，B兩點距離相等的M點對應的數；
（2）現在有一只電子螞蟻P從B點出發時，以3個單位/秒的速度向左運動，同時另一只電子螞蟻Q恰好從A點出發，以2個單位/秒的速度向右運動，設兩只電子螞蟻在數軸上的C點相遇，求C點對應的數是多少.
（3）若當電子螞蟻P從B點出發時，以3個單位/秒的速度向左運動，同時另一只電子螞蟻Q恰好從A點出發，以2個單位/秒的速度向右運動，求經過多長的時間兩只電子螞蟻在數軸上相距35個單位長度.
【答案】(1)40;(2)30;（3）經過13秒或27秒
【解析】
（1）先求出A、B兩點之間的距離：90-（-10）=100，再求出M點到A、B兩點的距離：100÷2=50，然后借助數軸即可求出M點．（2）根據A、B兩點的距離和兩只螞蟻的運動速度可求出相遇的時間，即可求出每個螞蟻運動的距離，即可求出C對應的數.（3）此問分為2只電子螞蟻相遇前相距35個單位長度和相遇后相距35個單位長度，分別計算即可.
（1）90-（-10）=100，
100÷2=50，
90-50=40.
答：M點對應的數是40.
（2）100（2+3）=20，
20
3=60，
90-60=30.
答：C點對應的數是30
（3）（100-35）÷（2+3）=13秒，
（100+35）÷（2+3）=27.
答：經過13秒或27秒兩只電子螞蟻在數軸上相距35個單位長度.
全優沖刺100分系列答案
英才點津系列答案科目：初中數學 來源： 題型：
【題目】有甲、乙兩個不透明的布袋，甲袋中裝有3個完全相同的小球，分別標有數字0，1，2；乙袋中裝有3個完全相同的小球，分別標有數字﹣1，﹣2，0．現從甲袋中隨機抽取一個小球，記錄標有的數字為x，再從乙袋中隨機抽取一個小球，記錄標有數字為y，確定點M坐標為（x，y）．
（1）用樹狀圖或列表法列舉點M所有可能的坐標．
（2）求點M（x，y）在函數y=﹣x2﹣1的圖象上的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A（m，m）在第一象限，且實數m滿足條件：
，ABy軸于B，ACx軸于C
（1）求m的值；
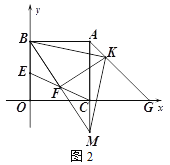
（2）如圖1，BE=1，過A作AF⊥AE交x軸于F，連EF，D在AO上，且AD=AE，連接ED并延長交x軸于點P，求點P的坐標；
（3）如圖2，G為線段OC延長線上一點，AC=CG，E為線段OB上一動點（不與O、B重合），F為線段CE的中點，若BF⊥FK交AG于K，延長BF、AC交于M，連接KM．請問∠FBK的大小是否變化？若不變，請求其值；若改變，求出變化的范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某活動中心準備帶會員去龍潭大峽谷一日游，1張兒童票和2張成人票共需190元，2張兒童票和3張成人票共需300元．解答下列問題：
（1）求每張兒童票和每張成人票各多少元？
（2）這個活動中心想帶50人去游玩，費用不超過3000元，并且出于安全考慮，兒童人數不能超過22人，請你幫助活動中心確立出游方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
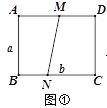
【題目】如圖①，矩形紙片ABCD的邊長分別為a、b（a＜b），點M、N分別為邊AD、BC上兩點（點A、C除外），連接MN．
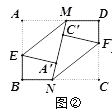
（1）如圖②，分別沿ME、NF 將MN兩側紙片折疊，使點A、C分別落在MN上的A′、C′處，直接寫出ME與FN的位置關系；
（2）如圖③，當MN⊥BC 時，仍按（1）中的方式折疊，請求出四邊形A′EBN與四邊形C′FDM 的周長（用含a的代數式表示），并判斷四邊形A′EBN與四邊形C′FDM周長之間的數量關系；
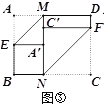
（3）如圖④，若對角線BD與MN交于點O，分別沿BM、DN將MN兩側紙片折疊，折疊后，點A、C恰好都落在點O處，并且得到的四邊形BNDM是菱形，請你探索a、b之間的數量關系.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】先化簡，再求值：
（1）（x+2）（x﹣3）﹣x（x﹣4），其中x=﹣ 
（2）（a+b）（a﹣b）+（a+b）2﹣2a2 ， 其中a=3，b=﹣ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某數學小組的10位同學站成一列做報數游戲，規則是：從前面第一位同學開始，每位同學依次報自己順序數的倒數的2倍加1，第1位同學報（ 
+1），第2位同學報（ 
+1），第3位同學報（ 
+1）…這樣得到的n個數的積為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】由于換季，一家服裝店的老板想將某服裝打折銷售，于是她和正在上七年級的兒子商量打折方案，下面是她和兒子商量時的對話情景：
媽媽：“兒子，每件衣服按標價的5折出售，可以嗎？”
兒子：“若每件衣服按標價的5折出售會虧本30元.”
媽媽：“那每件衣服按標價的8折出售呢？”
兒子：“若每件衣服按標價的8折出售將會賺60元.”
……
請根據上面的信息，解決問題：
（1）求這種服裝的標價.
（2）若要不虧本，至少打幾折？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等腰直角三角形
的直角頂點
在第一象限，頂點
、
分別在函數
圖像的兩個分支上，且
經過原點
，
與
軸相交于點
，連接
，已知平分四邊形
的面積.
(1)證明:
:
(2)求點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com